I am studying Deutsch's algorithm (elementary version of Deutsch-Josza) but I'm struggling with the actual implementation of the quantum oracle.
I understand the whole point of the algorithm and what it wants to achieve, i.e. to determine wether a function $f$ is constant or balanced with just one query on the function. However, I don't understand how one must implement the quantum oracle in order to get the algorithm working. We know that a quantum oracle is a black-box function that is used as input to another algorithm; we also know that there are four common functions used for demonstrating the Deutsch's algorithm: constant 1 (constant), constant 0 (constant), negation (balanced) and identity (balanced).
Based on that, take for example the constant 1 and negation: they could be implemented in Qiskit as following:
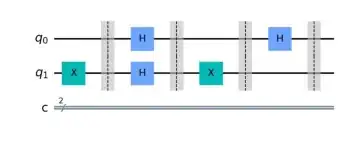 $f(x) = 1, \forall x \in \{0,1\}$" />
$f(x) = 1, \forall x \in \{0,1\}$" />
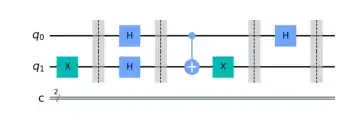 $f(x) = \neg x, \forall x \in \{0,1\}$" />
$f(x) = \neg x, \forall x \in \{0,1\}$" />
The first circuit implements the function $f(x) = 1$, whilst the second one the function $f(x) = \neg x$. What I don't understand is why the oracles (middle part of each circuit, wrapped by H gates) are different. If the oracle is a black-box function, it seems to me that it isn't so much black-box, as we need to know how to implement it based on the function we want to evaluate. Rather than understanding the algorithm itself, it seems that one must understand how to create the oracle, so what if we want to evaluate a more complex function?
Last but not least, if we look at $f(x) = 1, \forall x \in \{0,1\}$, we already know it is a constant function (same for $f(x) = \neg x, \forall x \in \{0,1\}$, we know at priori that it is a balanced function), so what is the point of creating an oracle and running it through Deutsch's algorithm?