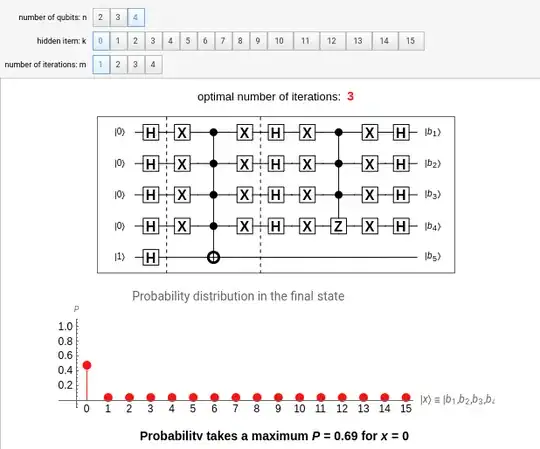
I am trying to understand Grover's algorithm. I read that this algorithm is able to find an entry in an unsorted list in just $\sqrt N$ steps, and needs only $\log N$ space.
I understand entanglement and superposition, and I also understand most parts of Shor's Algorithm. When it comes to Grover's algorithm, I often read that this algorithm uses an oracle. But as far as I understand, oracles do not really exist. They are used to describe hypothetical nondeterministic machines. But quantum computers do exist. The algorithm running on a real quantum computer will not really use a clairvoyant ghost who knows things nobody can know at this time.
So, how does it work?
I do not want to read scientific papers that deal with all the details. I just want a brief but correct overview.
Let's use an example: All 7 books about Harry Potter contain approximately 1 million words ($N = 1.000.000$). I want to know if the word "teapot" exists in one of the Harry Potter books, and if so, I want to get the position of at least one occurrence within the text.
If the word doesn't exist in the text, it will take me 1 million comparisons on a normal computer, i.e. 1 million steps. Grover will need only $\sqrt N = 1000$ steps to search through a list of $N = 1.000.000$ unsorted words. How?
Addendum
(reaction to comments)
I am not interested in an explanation about how the oracle works. I do not believe in fairies, elves or oracles. I believe in mathematics and physics. Oracles came into computer science when someone wanted to explain how nondeterministic machines like nondeterministic pushdown automatons will work. But nondeterministic machines do not exist in the real world. Even quantum computers aren't nondeterministic. So, there is no need to use fantasy beings with superpowers to explain quantum computers, since quantum computers do exist while wizards, magicians and oracles don't.
What I want is an explanation of grover's algorithm that uses only things that really exist in reality, i.e. quantum bits, superposition, entanglement, unitary operators etc. plus all the classic parts that still will be needed to sum up to the full algorithm.
And please use my Harry Potter example. If it's easier for you, let's assume that the word "teapot" exists exactly one times in the whole story, so that we know that there is exactly 1 needle in the haystack.
One thing that I do not understand, is this: How can the algorithm read all seven harry potter books (the complete haystack) and tell where exactly the word "teapot" is written using a number of steps that is proportional to the square root of the input length? How can the algorithm even read an input of $N$ items in a time proportional to $\sqrt N$?
Addendum II
I have learned form Norbert's Answer that Grover's Algorithm is unable to search for items in a database (like words in a list of words). So, what can it be used for? Norbert suggested, that Grover's Algorithm might give a square-root speed up for brute-force algorithms used to solve NP-Problems.
Traveling Salesmen is a problem in NP. How can you use Grover's Algorithm to find the shortest path?
If Traveling Salesman is not feasible, please use any other NP problem as an example, and please explain, how Grover's Algorithm can be used to solve it.
I still want to have a brief explanation of Grover's Algorithm (i.e. Grover's algorithm in a nutshell) but didn't get a sufficient answer yet.