In many quantum algorithms, we need to compute the expectation value $\langle\psi|U|\psi\rangle$, where $U$ is an $n$-qubit unitary operator and $|\psi\rangle$ is an $n$-qubit state. The Hadamard test is a quantum algorithmic primitive used to compute this expectation value using one ancilla qubit and some controlled operations[1],[2].
And since $U$ is generally not Hermitian, the expectation value can be a complex number. The Hadamard test is able to measure the real and imaginary parts in two separate measurements.
In Hadamard test we use the following circuit for estimating the real part of $\langle\psi|U|\psi\rangle$
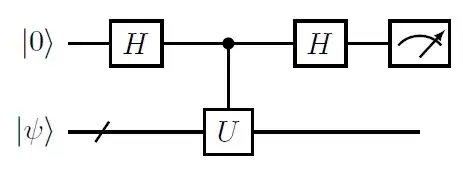
You can easily verify that the probability of measuring the ancilla qubit to be in state $|0\rangle$ equals $\frac{1}{2}(1+\mathrm{Re}[\langle\psi|U|\psi\rangle])$
Similarly, we use the following circuit for estimating the imaginary part

where $S$ is the phase gate.
$$S = \begin{pmatrix}1 & 0 \\ 0 & i \end{pmatrix}$$
The probability of measuring the ancilla qubit to be in state $|0\rangle$ equals $\frac{1}{2}(1+\mathrm{Im}[\langle\psi|U|\psi\rangle])$
To compute the expectation value with absolute error $\epsilon$ we need to repeat this procedure $\mathcal{O}(1/\epsilon^2)$ times.
Hadamard test is part of many algorithms. For example:
- If $|\psi\rangle$ equals the basis state $j$, Hadamard test can be use to get the diagonal element $u_{jj}$ for the matrix $U$. This technique used in Aharonov–Jones–Landau algorithm to compute the Jones polynomial of the plat closure of a braid[3].
- We can use Hadamard test to compute the trace of the matrix $U$ by choosing $|\psi\rangle$ to be the maximally mixed state. This technique used by Shor and Jordan to compute the Jones polynomial of the trace closure of a braid in the DQC1 model of computation[4].
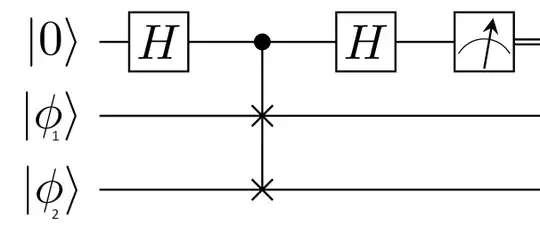
- If $|\psi\rangle=|\phi_1\rangle|\phi_2\rangle$, and $U$ is the $n$-qubit SWAP gate, the probability of measuring the ancilla qubit to be in state |0⟩ equals $\frac{1}{2} + \frac{1}{2}|\langle\phi_1|\phi_2\rangle|^2$. So, we can use this circuit to estimate the overlap of two the quantum states $|\phi_1\rangle$ and $|\phi_2\rangle$. This is known as the swap test. It is commonly used in quantum machine learning[5].
- Hadamard test is also used to approximate tensor network contraction[6], to extract information about the gradient of the objective function in variational algorithms[7], ...etc.
[1] Childs. Lecture Notes on Quantum Algorithms.
[2] Lin. Lecture Notes on Quantum Algorithms for Scientific Computation.
[3] Aharonov, Jones and Landau. A Polynomial Quantum Algorithm for Approximating the Jones Polynomial
[4] Shor and Jordan. Estimating Jones polynomials is a complete problem for one clean qubit
[5] https://en.wikipedia.org/wiki/Swap_test
[6] Arad and Landau. Quantum computation and the evaluation of tensor networks.
[7] Harrow and Napp. Low-depth gradient measurements can improve convergence in variational hybrid quantum-classical algorithms


