Confusion on computing matrix elements with quantum circuits

Question

Let us a consider a $N$ qubit quantum system and an obervable $O$. In general one would be interested in computing something like $\langle O \rangle$ using a quantum computer. In a problem I am interested in, however, for the given Hermitian operator $O$ and a family of unitaries $\{ U_a \}_{a \in \mathbb{N}}$ I am interested in computing stuff like

$$ \langle 0 | U^\dagger_a O U_b | 0 \rangle \equiv \langle a | O | b \rangle. $$

This, I believe would be in general called a matrix element (please correct if me if wrong). Now, I am curious to as to how one goes to compute such a complex number on a circuit model.

I do think that we need to implement the followong:

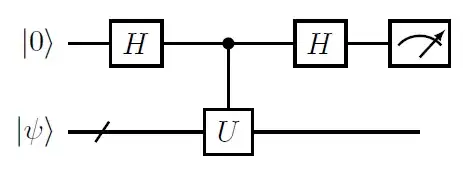
• First we need some ancilla qubit. We start with one ancilla qubit in the state $|0\rangle$. Apply $H$ to this ancilla so it enters the superposition.

• Then we prepare the $N$‑qubit system register in the state $|b\rangle$ (i.e., the “input” state).

• Now controlled‑$U$ operation. I can use the ancilla to control $U$ on the system: If the ancilla is in $|1\rangle$, $U$ is applied on the system and if it’s in $|0\rangle$, nothing happens so that the joint state becomes
$(1/\sqrt{2})[|0\rangle \otimes |b\rangle + |1\rangle \otimes U|b\rangle]$.

• Then we need a basis rotation on the system. We apply an additional unitary transformation $U_a^\dagger$ on the system register that “rotates” the target state $|a\rangle$ into a standard basis state (so we map $|a\rangle \to |0…0\rangle$). That is, after this operation, the overlap $\langle a|…\rangle$ is translated into an amplitude for measuring $|0\ldots 0\rangle$ in the system.

• System measurement (postselection). Finally, we measure the system register in the computational basis, and postselect on the outcome corresponding to the rotated state (for example, $|0\ldots 0\rangle$ ). Postselection isolates the components of the system that are aligned with $|a\rangle$, so that the amplitudes associated with $|0\ldots 0\rangle$ now encode $\langle a|b\rangle$ and $\langle a|U|b \rangle$ from the two branches.

• We now apply a second $H$ gate on the ancilla. This one interferes the two ancilla branches: one branch where the system stayed at $|b\rangle$ and one where it evolved to $U|b\rangle$. The interference converts the relative phase and amplitude difference (i.e. the difference between $\langle a|b \rangle$ and $\langle a|U|b\rangle$) into a measurable difference in the ancilla’s state.

• Final measurement and data extraction is the last step then where we measure the ancilla in the computational basis to construct empirical statistics and average the results to accurately extract the desired matrix element.

To be honest I am not 100% sure this makes sense (even if the name "matrix element makes sense here) so I would appreciate some help.

Answer 1

You are right about the extraction of the desired matrix element.
We have the hadamard test circuit

Start with your equaition:\ $1/\sqrt{2})[|0\rangle \otimes |b\rangle + |1\rangle \otimes U|b\rangle]$
I will use $| \phi\rangle $ instead of b and $|0\rangle$ so the joint state becomes: $ \frac{1}{\sqrt{2}}\Big(|0\rangle \otimes |\psi\rangle \;+\; |1\rangle \otimes U|\psi\rangle\Big)\,. $ The final joint state (after the second Hadamard) is:

$ \frac{1}{\sqrt{2}}\Big[\;\frac{1}{\sqrt{2}}\big(|0\rangle+|1\rangle\big)|\psi\rangle \;+\; \frac{1}{\sqrt{2}}\big(|0\rangle - |1\rangle\big)U|\psi\rangle\;\Big]\,, $ which we can simplify as: $ \frac{1}{2}\Big[\,|0\rangle\otimes\!(|\psi\rangle + U|\psi\rangle) \;+\; |1\rangle\otimes\!(\,|\psi\rangle - U|\psi\rangle)\Big]\,. $
Now we measure the ancilla qubit in the $\{|0\rangle,|1\rangle\}$ basis. The probability of each outcome can be computed from the final state above by taking the norm squared of the corresponding branch:
Probability ancilla = $|0\rangle$: $ P(0) = \Big\|\,\frac{1}{2}\, (|\psi\rangle + U|\psi\rangle)\Big\|^2 \;=\; \frac{1}{4}\,\langle \psi| (I + U^\dagger)(I + U) |\psi\rangle\,, $
This simplifies to $ P(0) =\; \frac{1}{2}\Big(1 + \mathrm{Re}\,\langle\psi|U|\psi\rangle\Big)\,. $
The result is also found in this post What is a hadamard test

The measurement outcome for the ancilla can be treated as a random variable $Z_{\text{anc}}$ that takes value $+1$ if the ancilla is found in $|0\rangle$ and $-1$ if found in $|1\rangle$. From the probabilities derived, the expected value of this random variable is $ \mathbb{E}[Z_{\text{anc}}] \;=\; (+1)\,P(0) + (-1)\,P(1) \;=\; P(0) - P(1). \ $This is how we can compute matrix elements on a quantum computer: it turns an inner product containing a unitary into an observable (the ancilla’s $Z$) that we can measure. If in our problem we want to compute $\langle a|O|b\rangle$, we would identify $|\psi\rangle$ and $U$. Then we have: $|\psi\rangle = |b\rangle = U_b|0\rangle$ and $U = U_a^\dagger O U_b$. Then $\langle \psi|U|\psi\rangle = \langle b|\,U_a^\dagger O\,U_b\,|b\rangle = \langle a|O|b\rangle$.

Answer 2

The universal quantum computer model proposed by Deutsch (1985) is to use a unitary transformation $U$ to transform state $|a\rangle$ to state $|b\rangle$. The unitary transformation and thus the matrix contains the problem you try to solve/compute.

Designing the matrix is the job of your algorithm -- often a hard one. If your problem is to find the factors of a large number, your matrix probably needs to compute $a^x (mod M)$ and get the order number encoded in $|b\rangle$. That's the matrix of Shor's algorithm.

$|a\rangle$ encodes your input number or numbers. (The input of Shor's algorithm contains many $x$ in one stroke.) $|b\rangle$ encodes the result that you seek. To get an accurate result - to avoid uncertainty, $|b\rangle$ has to be an eigenstate of your measurement $O$.

One qubit has 2 eigenstates -- $|0\rangle$ and $|1\rangle$. With $N$ qubits, you have $2^N$ eigenstates. The number of qubits depends on the dimension of your problem-matrix $U$. If $N$ is bigger than what you need for the input or output, you probably are using ancillary qubits in your algorithm.

Having the final state $|b\rangle$ being an eigenstate is the difficult part of algorithm design. Sometimes, you have to play tricks to get around it. In Shor's algorithm, the final state $|b\rangle$ is not an eigenstate of the measurement $O$. However, the eigenstate that a measurement collapses to is close to the solution. So, collapsing measurement is a trick often played by quantum algorithms.