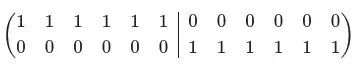For the famous $[\![4, 2, 2]\!]$ code, there is a circuit to encode two physical states into the logical state (from Roffe's work):
As $[\![m, m-2, 2]\!]$ is a class of error-detection code, I am wondering if there is a known similar encoding circuit for $[\![6, 4, 2]\!]$ code. Mathematically, the unitary always exists. But I failed to find any similar explicit circuit from the existing literature.
We can obtain an encoding circuit for the $[\![m,m-2,2]\!]$ code for any even $m$ by generalizing the circuit displayed in the question. More precisely, for every new qubit we prepend a CNOT gate with the new qubit as the control and the second from the bottom qubit as the target and append a CNOT gate with the bottom qubit as the control and the new qubit as the target.
We can verify that the circuit is correct by propagating $I^{\otimes m-2}\otimes Z\otimes I$ and $I^{\otimes m-2}\otimes I\otimes Z$ through the circuit and checking that we obtain the appropriate stabilizer generators $Z^{\otimes m}$ and $X^{\otimes m}$.
This can easily be done using stac. More explanations of the process for generating the encoding circuit is explained in a previous answer. But, since, this question is specifically asking for $[[2m, 2m-2, 2]]$ codes, here is how to do it.
import stac
import numpy as np
m = 3
generator_matrix = np.zeros((2*2*m, 2), dtype=int)
generator_matrix[0, :2*m] = np.ones((2*m,))
generator_matrix[1, 2*m:] = np.ones((2*m,))
stac.print_matrix(generator_matrix, augmented=True)
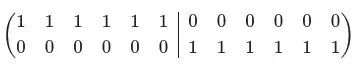
code = stac.Code(generator_matrix)
code.construct_encoding_circuit()
code.encoding_circuit
0 CX (0, 0, 2) (0, 0, 1)
1 CX (0, 0, 3) (0, 0, 1)
2 CX (0, 0, 4) (0, 0, 1)
3 CX (0, 0, 5) (0, 0, 1)
H (0, 0, 0)
4 CX (0, 0, 0) (0, 0, 1)
5 CX (0, 0, 0) (0, 0, 2)
6 CX (0, 0, 0) (0, 0, 3)
7 CX (0, 0, 0) (0, 0, 4)
8 CX (0, 0, 0) (0, 0, 5)
code.encoding_circuit.draw()
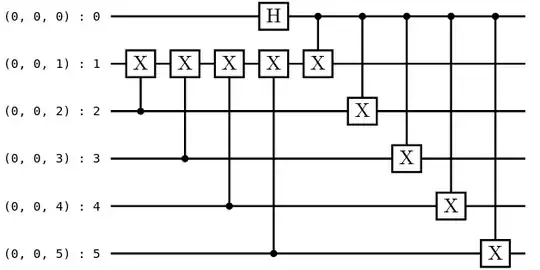
Here the input state is inserted onto the bottom $2m-2$ qubits.
