Why do shadows from the sun join each other when near enough?

Question

I was laying on my bed, reading a book when the sun shone through the windows on my left. I happened to look at the wall on my right and noticed this very strange effect. The shadow of my elbow, when near the pages of the book, joined up with the shadow of the book even though I wasn't physically touching it.

Here's what I saw:

The video seems to be the wrong way up, but you still get the idea of what is happening.

What is causing this? Some sort of optical illusion where the light gets bent? Coincidentally, I have been wondering about a similar effect recently where if you focus your eye on a nearby object, say, your finger, objects behind it in the distance seem to get curved/distorted around the edge of your finger. It seems awfully related...

EDIT: I could see the bulge with my bare eyes to the same extent as in the video! The room was well light and the wall was indeed quite bright.

Answer 1

As said by John Rennie, it has to do with the shadows' fuzzyness. However, that alone doesn't quite explain it.

Let's do this with actual fuzzyness:

I've simulated shadow by blurring each shape and multiplying the brightness values¹. Here's the GIMP file, so you can see how exactly and move the shapes around yourself.

I don't think you'd say there's any bending going on, at least to me the book's edge still looks perfectly straight.

So what's happening in your experiment, then?

Nonlinear response is the answer. In particular in your video, the directly-sunlit wall is overexposed, i.e. regardless of the "exact brightness", the pixel-value is pure white. For dark shades, the camera's noise surpression clips the values to black. We can simulate this for the above picture:

Now that looks a lot like your video, doesn't it?

With bare eyes, you'll normally not notice this, because our eyes are kind of trained to compensate for the effect, which is why nothing looks bent in the unprocessed picture. This only fails at rather extreme light conditions: probably, most of your room is dark, with a rather narrow beam of light making for a very large luminocity range. Then, the eyes also behave too non-linear, and the brain cannot reconstruct how the shapes would have looked without the fuzzyness anymore.

Actually of course, the brightness topography is always the same, as seen by quantising the colour palette:

---

¹To simulate shadows properly, you need to use convolution of the whole aperture, with the sun's shape as a kernel. As Ilmari Karonen remarks, this does make a relevant difference: the convolution of a product of two sharp shadows $A$ and $B$ with blurring kernel $K$ is

$$\begin{aligned} C(\mathbf{x}) =& \int_{\mathbb{R}^2}\!\mathrm{d}{\mathbf{x'}}\: \Bigl( A(\mathbf{x} - \mathbf{x}') \cdot B(\mathbf{x} - \mathbf{x'}) \Bigr) \cdot K(\mathbf{x}') \\ =& \mathrm{IFT}\left(\backslash{\mathbf{k}} \to \mathrm{FT}\Bigl(\backslash\mathbf{x}' \to A(\mathbf{x}') \cdot B(\mathbf{x}') \Bigr)(\mathbf{k}) \cdot \tilde{K}(\mathbf{k}) \right)(\mathbf{x}) \end{aligned} $$

whereas seperate blurring yields

$$\begin{aligned} D(\mathbf{x}) =& \left( \int_{\mathbb{R}^2}\!\mathrm{d}{\mathbf{x'}}\: A(\mathbf{x} - \mathbf{x}') \cdot K(\mathbf{x}') \right) \cdot \int_{\mathbb{R}^2}\!\mathrm{d}{\mathbf{x'}}\: B(\mathbf{x} - \mathbf{x'}) \cdot K(\mathbf{x}') \\ =& \mathrm{IFT}\left(\backslash{\mathbf{k}} \to \tilde{A}(\mathbf{k}) \cdot \tilde{K}(\mathbf{k}) \right)(\mathbf{x}) \cdot \mathrm{IFT}\left(\backslash{\mathbf{k}} \to \tilde{B}(\mathbf{k}) \cdot \tilde{K}(\mathbf{k}) \right)(\mathbf{x}). \end{aligned} $$

If we carry this out for a narrow slit of width $w$ between two shadows (almost a Dirac peak), the product's Fourier transform can be approximated by a constant proportional to $w$, while the $\mathrm{FT}$ of each shadow remains $\mathrm{sinc}$-shaped, so if we take the Taylor-series for the narrow overlap it shows the brightness will only decay as $\sqrt{w}$, i.e. stay brighter at close distances, which of course surpresses the bulging.

And indeed, if we properly blur both shadows together, even without any nonlinearity, we get much more of a "bridging-effect":

But that still looks nowhere as "bulgy" as what's seen in your video.

Answer 2

It's because the Sun is not a point source, so the edges of the shadows are slightly fuzzy. This is my rather crude attempt to show why this happens:

There are far better diagrams in the Wikipedia article on the umbra that explains what is going on. The fuzzy bit at the edge of the shadow is called the penumbra.

The reason you see the bulge where the shadows approach is due to the penumbra and the fact that the human eye isn't that great at handling contrast. As the two shadows approach, but before they touch, their penumbras (penumbrae?) overlap. This means the region between the shadows is darker than the rest of the penumbra. Another rather crude diagram follows:

This isn't a great diagram because the density of the penumbra isn't constant, but rather shades from black to white across its width. However Google Draw doesn't do gradient fills so I'm stuck with a rather poor representation. Anyhow, it should hopefully be obvious that where the penumbras overlap they darken each other, so the region between the two shadows gets darker. Because the eye isn't good at handling a wide contrast range it looks as if the shadows have grown a bulge towards each other.

Answer 3

I believe you'll find the cause is diffraction, as described in this article. The photo shows a similar effect when holding two fingers close together.

Black Drop Effect described in Sky and Telescope

As you bring your elbow and book together, you're creating a diffraction pattern as can be seen in the image in the article below, a brighter light in the middle with black bands on either side. As you bring them even closer together, the black bands grow closer together. This is why they appear to suddenly "jump" towards each other.

Image of standard diffraction pattern

Answer 4

Unfortunately, all of the highly upvoted answers to this question are wrong.

One of them says that it's a diffraction effect. It's actually wholly explainable by geometric optics.

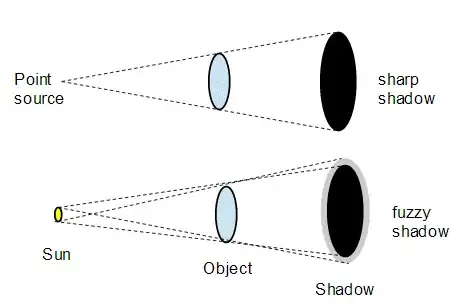
The other two (John Rennie's and the accepted community wiki) say that the bulge is in the penumbra, and it appears as dark as the umbra because the eye/camera can't distinguish the dark levels very well. Actually, the umbra bulges. The penumbra adds to the effect, but not very much:

(I added a blue tint to the umbra.) Note also that the bulge is unilateral. None of the other answers mention that effect, but you can see it in the video in the question, and in this question, and in the video linked from this question. I'll get back to it in section 2.

The reason the penumbra looks so much darker in the community-wiki answer is that those images are incorrectly calculated – see section 3.

1. Shadows of objects equidistant from the screen

Here's a simulation of the shadow of two discs, one 10× the radius of the other, illuminated by the sun (a disc at infinity). I added a slight blue tint to the umbra.

It's easier to understand what's going on if you look at the shadow of the same objects illuminated by a point source:

It looks like the discs are still well separated when the umbras start to bulge, but actually they are so close together that they overlap.

I think it's easy to make the mistake of thinking that the umbra is the shadow you would get with a point source, and the penumbra is "extra". If that were true, then the bridging would have to be an effect of the penumbra, because you can't have complete blockage of the light in the middle when there is still a gap between the discs. In reality, the umbra is misleadingly small, and the penumbra appears too thin to make up the difference (when correctly calculated – see section 3), so objects seem farther apart then they really are. The bulging effect is, in some sense, the breakdown of that illusion.

2. Shadows of objects at different distances from the screen

When the objects are at different distances, something interesting happens:

It's not hard to understand why only one side bulges. Call the disc farther from the screen F and the nearer one N. There is a range of separations at which F's thicker penumbra reaches N's umbra, but N's thinner penumbra doesn't reach F's umbra. In the intersection of the penumbras, there is a subregion where both discs together completely block the light (additional umbra of the combined shadow). That region touches N's umbra, but it can't reach F's:

UUUUUUUUUUUpppppppp             <-- shadow of F alone
             ppppUUUUUUUUUUU    <-- shadow of N alone
UUUUUUUUUUUpppUUUUUUUUUUUUUU    <-- combined shadow

3. Linear-light versus perceptual blurring

Human brightness perception is nonlinear, and sRGB is nonlinear to match it: a disproportionately large fraction of the RGB cube is allocated to dim colors. Shadow calculation should be done in terms of light energy, ignoring human psychology. This turns out to make a large difference:

A lot of image processing software gets this wrong. Eric Brasseur wrote a long rant about it years ago, which seems to have had some effect. The problem is fixed in Gimp since version 2.10 (which was released in 2018, after the community-wiki answer was written).

The community wiki's images are actually wronger than my wrong image, since they use a Gaussian kernel ("Gaussian blur" in Gimp) instead of a uniform disc ("lens blur"), but I think that doesn't affect the result as much.

Answer 5

It's the shadow blister effect. See my answer to the same question posted more recently here.

Answer 6

I do not guarantee this is the correct answer, but you can verify it practically.

The light rays causing the shadow of your hand and that of your book, are not parallel. The bulging of shadows as they are near each other, means that both the bulged shadows are of the elbow. So, at the point when your elbow is near your book, two light sources (or bending of light such that unparallel rays of light act on the elbow causing two shadows) are acting on the elbow.

I think you too have guessed this.You can verify it by doing two things:

1. Opening the window so that direct light can fall. This will tell if bending is caused by the glass window.
2. Change of height of the book and the elbow wrt. the window. Try to see if the effect is observed at all heights.

Answer 7

Coincidentally, I have been wondering about a similar effect recently where if you focus your eye on a nearby object, say, your finger, objects behind it in the distance seem to get curved/distorted around the edge of your finger. It seems awfully related...

You are right they are related. This is another diffraction effect. You are seeing single edge diffraction, also known as the knife edge effect. Here is a web page describing it.

Light passing very near your finger is deflected. Since the direction has changed, it appears to come from a different place.

Answer 8

Try this out in a room that has one of those ceiling fans with four light bulbs. The multiple sources of light produce multiple shadows that are clearly visible and you can see this sort of phenomenon take effect. As the shadows overlap it gives this appearance and produces the phenomena spoken of. In normal situations the multiple sources of light encountered can often times be light that is reflected off of walls and nearby objects, anything that is white or lighter colored. The multiple shadows produced are so faint they are not even noticeable until they overlap other shadows. Sources of light from different angles produce multiple shadows. When your elbow moves toward the book, for example, multiple shadows from both objects overlap where they appear to combine. What looks like the edge of the shadow of a single object is the edge of where the layers of shadows overlap each other the most.