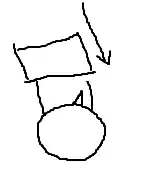
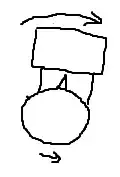
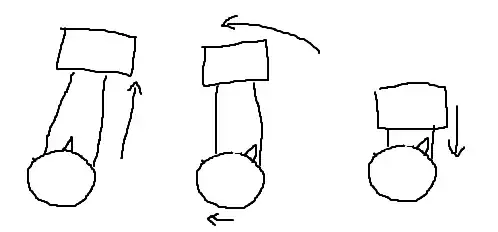
Other answers have pointed out other ways that might be more efficient, but one very simple way to do it is as follows: start with both arms parallel to the body. Then swing them both backward, up over the head, and then back down in front of the body, leaving them back in the starting position. After this manoeuvre, the body will be oriented in a slightly different position, with the feet slightly further forward than they were before, and the head slightly further back. It can be repeated to produce a larger change in orientation, or performed in reverse to rotate in the opposite direction.
It might seem as if this shouldn't work, but if we consider the conservation of angular momentum, we can see that it has to. When the astronaut starts moving her arms, she gives them some angular momentum. This means that her body's angular momentum changes by an equal and opposite amount. Because her body has a larger moment of inertia than her arms, its angular velocity will be smaller, because $\omega = L/I$. This means that once her arms have completed a full revolution, her body's orientation will have changed by only a small (but non-zero) angle. When she stops moving her arms, angular momentum is transferred in the opposite direction, and the body's angular momentum again becomes zero.
The amount of rotation this move produces can be increased by tucking the legs into the body, reducing its overall moment of inertia. As dmckee points out in a comment, this technique is used by springboard divers to perform half-twist moves, so we know that it definitely works, and if performed correctly can be quite efficient. (Doing it effectively while encumbered by a pressure suit might be a different matter, however.)
Bonus edit: the technique is demonstrated in zero-G conditions (aboard Skylab) starting at 0:50 in the following video:
https://youtu.be/RjvmXLyrtjM