1

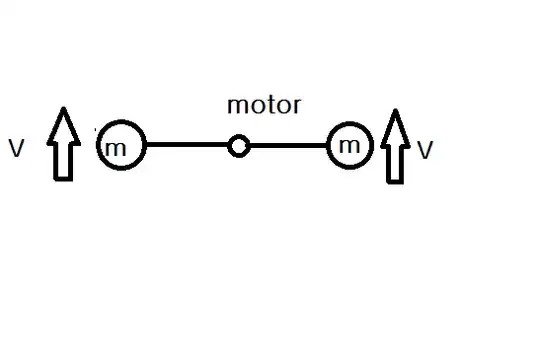
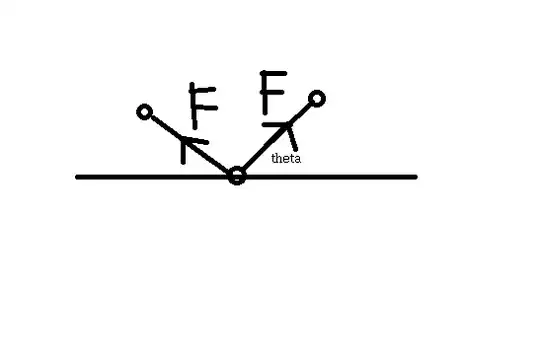
Let say the motor makes the two rigid body rotate as a same velocity. (they rotate the opposite direction) then the Net force of the motor is 2Fsin(Theta). The acceleration of the motor is 2Fsin(theta)/M. (M is the mass of the motor) Then, the motor's velocity is always >=0. so, the motor can move. the motor's power is the inner force of the system, but it made the system move! how can this be?

Qmechanic
  • 220,844
Yun Hoo
  • 63
  • 5

2 Answers2

1

Whilst the motion you intend is not altogether clear, the motor will indeed move as you say. But the attached rigid bodies also move, such that the center of mass of the whole system is stationary (or, more precisely, its state of motion unperturbed by the system's internal motions). Work out the path of the center of mass in your system to check this assertion. In particular, you should see that the motions of motor and attached masses will be in opposite directions, if you apply Newton III to the system parts properly.

It is also true that cyclic configuration changes of a deformable system (which this is) in general leave the system with a nett rotation when the system gets back to its initial configuration, even though angular and linear momentum of the whole system are conserved at all times. This is, for example, how a cat flips over to land on its feet when in freefall. See for example the answers to the Physics SE Question "Is there a way for an astronaut to rotate?". There's also some interesting discussion of this on Space Exploration Stack Exchange Here.

Community
  • 1
Selene Routley
  • 90,184
  • 7
  • 198
  • 428
0

You say:

the motor's velocity is always $>=0$

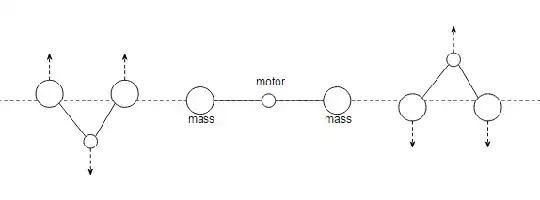
but this is not true. The magntude of the velocity is indeed always greater than or equal to zero, but velocity is a vector so the direction matters as well. The motor will oscillate alternately up and down as the masses rotate around it. The combined centre of mass of the motor and the two masses will always stay in the same place.

This is my somewhat crude attempt to show how the motor and masses move. The dashed line shows where the centre of mass is. This assumes the masses weigh more than the motor, so the motor moves more than the masses do:

Motion

John Rennie
  • 367,598