Why does a helium filled balloon move forward in a car when the car is accelerating?

Question

I noticed that when I had a helium filled, latex balloon inside of my car, it moved forward in the cabin as I accelerated forward. The faster I accelerated forward, the faster the balloon went from the back of the car to the front of the car. The balloon didn't have a string. This became a game with my 4 year old as we drove home. We figured out where the balloon would go based on how fast I accelerated, turned corners etc. I expected that it would act a lot like the water in a cup does, but it was the total opposite it seemed. What forces caused this behavior? I assumed it has something to do with the fluid dynamics in the closed cabin, but I can't figure it out.

Answer 1

It travels forwards instead of backwards in an accelerating car for the same reason that a helium balloon travels upwards instead of downwards under the influence of gravity. Why is that?

In an accelerating car, for all intents and purposes the acceleration can be considered a change in the amount and direction of gravity, from pointing straight down to pointing downwards and backwards. The balloon doesn't know and doesn't care if the acceleration is from gravity or from the acceleration of the car; it just tries to move in the direction it naturally moves, namely, against the direction of the acceleration. Thus, it moves forwards when you accelerate. Hopefully you find this explanation intuitively satisfying.

Another more rigorous way to view the problem is through Lagrangian minimization. The balloon can be considered a low-density object embedded in a higher-density fluid constrained within the confines of the car. Under the influence of gravity pointing sideways, the total system potential energy decreases the farther forward the balloon is situated. Since the force is the gradient of the potential, the balloon will try to move forward.

Answer 2

When your car accelerates forward, the air inside moves back relative to the car. This creates a slightly high pressure in the rear of the vehicle and a low pressure up front.

Since helium is lighter than air, it moves away from the region of high pressure. A similar balloon filled with $CO_2$ would move back, since it is heavier than the surrounding air

Answer 3

Fun question. Here's my "me-too" answer.

Suppose the car has just emerged from a river, so there's a lot of water in it, and the balloon is tied to the floor.

Then you drive away.

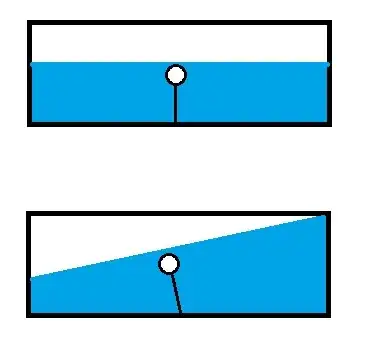
The air in the car is just like a bunch of water :)

Answer 4

It acts precisely like water in a cup. Or, more specifically, like the air in the cup. Since the helium is a much lower density than the nitrogen and other gasses in your car, it can be visualized like an air bubble in a bottle. The container for the helium(the balloon) has negligible mass.

When you accelerate forward, the water in a bottle will move backwards, just like you'd expect. The air bubble will appear to move forward to fill that void left by the water, just like the helium balloon.

Additional forces may come into play as well. There is friction from the rubber on the ceiling. Also, when you accelerate, the center of gravity of your car moves backwards on the wheelbase. The nose of your car lifts, and the tail of your car sinks. When you stop, the opposite happens, and when you turn left, your car leans right, as you can feel. This may tilt the ceiling allowing the balloon to move in response to the tilted ceiling. This could have an effect as well.

Answer 5

I am not good at explaining things but here it goes

try to understand it this way

assume the rectangle to be you car, now the dotted area is filled with normal air and their is a helium balloon in between

So when you accelerate everything in the car tries move backward with respect to the car even the helium balloon, so then why the balloon goes forward,

As you may know helium is less denser than the air and so it is lighter then the air, so when you accelerate the air starts moving backwards but as the helium is lighter it is pushed forward by the air collecting at its back the same phenomenon when you fill a bucket and a ball kept at its bottom starts rising up because it is less denser than water.

Answer 6

When you're in an accelerating frame of reference, the acceleration is perceived as gravity. For instance in an accelerating train, you stand on an angle, in the direction of motion. It feels like you're on a slope, and de facto, you are.

The helium-filled ball is simply moving against the direction of what looks like gravity: the same thing that it does when you're not in an accelerating frame. It does that for the same reason: buoyancy due to being lighter than air.

When you let go of the balloon in an accelerating train, it will not move directly forward, but on an angle: forward and up. That is the same angle at which you stand, if you balance without support. If while standing in this position you hold a balloon on a string, the string will point in the same direction, parallel to your body, and if you let go of the balloon, it will move in that direction. That is the direction which corresponds to "up", slanted due to the vector combination of the force of gravity (which acts on you downward perpendicularly to the floor) and the fictitious force which appears to be pulling you backwards due to acceleration.

So, in summary:

1. A balloon rises "up" due to buoyancy.
2. What determines which way is up "up" is a vector combination of gravitational pull, and the fictitious force caused by acceleration, which mimics gravity.

Answer 7

I wondered this myself...

Then it hit me, the analogy in my head of a ball rolling on a surface was wrong... the balloon isn't something floating in nothing, it is a body that is less massive than the air it is displacing.

So when you break, everything tries to move forward, but the air wins because it has more inertia, and the balloon is forced backwards.

it is essentially the same thing as what normally happens with a ballon, only with the vectors turned on their side... normally all air and balloons and helium are pulled to the earth, but since the air is more dense it is pulled more... and displaces the balloon with the helium.

Answer 8

The simplest way to think about the helium balloon in the accelerating car is to invoke Einstein's Principle of Equivalence: a constant acceleration is the same, in all respects, as a gravitational force. To make matters as simple as possible, we'll ignore the real force of gravity (i.e. what's pulling the car toward the Earth) and just think about the forward acceleration of the car. According to the Principle of Equivalence, the effect of this acceleration is exactly the same as a gravitational force pointing to the rear of the car. But everyone knows what a helium balloon, immersed in air, does in the presence of gravity: it rises, i.e. it moves in the direction opposite to the gravitational force.

So when the car accelerates, the balloon moves forward. Incidentally, the Principle also explains why, when the car accelerates, a passenger is jerked backwards: because, unlike the balloon, the passenger falls downward, in the same direction as the gravitational force.

In answering this question, I'm assuming you accept that a helium balloon rises in the presence of Earth's gravity. Because helium has a smaller density than air, the buoyant force of air will push it toward the sky against gravity

Answer 9

The answer that makes the most sense to me is based on exercise 88 in chapter 12 of University Physics by Young and Freedman (13th Ed.):

Consider a tube of air with cross-sectional area $A$ extending from the windshield to the back. Suppose the pressure at the front of the tube is $p_0$. Consider some section of this tube a distance $x$ from the windshield with width $\Delta x$. Let the pressure on the front be $p$ and the pressure at the back $p+\Delta p$. So there's a force on the front of this volume of air of magnitude $pA$ (pressure is force per unit area) and there's a force on the back of magnitude $pA+\Delta p A$. So, the net horizontal force on it is $\Delta p A$ towards the windshield. The mass of this volume is just $A\Delta x \rho$, where $\rho$ is the density of the air. So, by Newton's second law, you get $$\Delta p A = A \rho \Delta x a$$ which we can rearrange to get $$\frac{\Delta p}{\Delta x} = \rho a$$ We're assuming here that the density of the air is constant, which isn't strictly true but it doesn't change all that much for like, a normal acceleration a car might have so it's a decent approximation. You can take the limit of the above expression as $\Delta x \to 0$ to get $$\frac{dp}{dx}=\rho a$$ So the pressure increases linearly with distance as you go back in the car, so we get $p(x)= p_0 + \rho a x$. Notice that this is very similar to how pressure behaves as you go deeper underwater.

Using the same reasoning as in the archimedes principle, imagine some volume $V$ in the car. The net horizontal force on it depends on the pressure gradient of the car and its surface, so it'll be the same if the volume contains air or if it contains a balloon. Suppose this force has magnitude $F$. If it's air, this net force keeps it accelerating with car, so by Newton's second law, we have $$F=\rho V a$$ because its mass is $\rho V$. If this same force acts on a balloon with average density $\rho_{b}$, then by Newton's second law again, we have $$\rho V a = \rho_b V a_b$$ where $a_b$ is the acceleration of the balloon (wrt to the ground). We can rearrange this to get $$a_b = \frac{\rho}{\rho_b} a$$ Since the car has acceleration $a$, the relative acceleration of the balloon wrt to the car is $$a_b-a=\left( \frac{\rho}{\rho_b}-1 \right)a$$ So, if the balloon is lighter than air, like a helium balloon is, then it will have an acceleration forward relative to the car, and if it's heavier, it'll have an acceleration backward relative to the car.

PS: I know this is a very late response but I was looking around on the internet to check my answer to this question and couldn't find anything outside of chegg/numerade/etc. so I thought I'd post it here for anyone else in the future looking for the same, hope necroposting isn't against the rules.