Intuition:
What happens depends on the ratio of the densities of the air filled in the balloon and the air outside the balloon.
When the truck accelerates, the air moves towards the back of the truck and this causes the air pressure at the back of the truck to be greater than the pressure of the air at the front of the truck. As there is a pressure gradient, there will be buoyant forces.
As the higher pressure is at the back side of the truck, the buoyant forces will be operating in in the back to front direction.
How does it move depends on which forces wins: the buoyant force or the pseudo force.
Mathematical details:
Let the box shown below represent the truck.
Let $\theta$ be the angle between the string connecting the balloon to the ceiling and the normal draw from the pivot (as shown in the figure).
Let $T$ be the tension in the string connecting the balloon to the ceiling.
Let $a$ be the acceleration of the truck.
Let $\rho$ and $\sigma$ be the density of the air outside the balloon and the air inside the balloon respectively.
Let $m$ and $V$ be the mass and volume of the balloon.
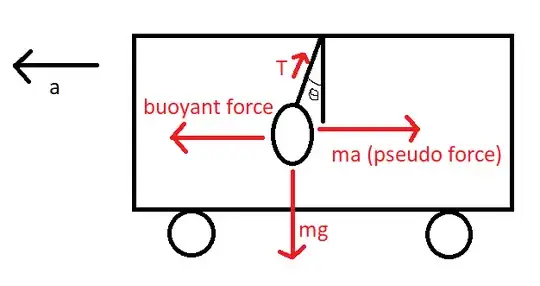
We will solve the problem from the frame of reference of the truck. As such a frame is non-inertial, a pseudo force in the direction opposite to that of the acceleration will be acting on every object.
We can write the force equations in the two components (x-axis and y-axis).
As the balloon does not fall down or rise up, the vertical component of the tension must completely cancel the weight.
$$T \cos \theta = mg \implies T = \frac{mg}{\cos \theta} \tag{1}$$
After a some time since the truck started accelerating, the balloon would have reached an equilibrium position. The net force in the horizontal direction is therefore zero.
The sources of force in the horizontal direction are pseudo force, buoyant force and the tension in the string. After accounting for the direction of the aforementioned forces, we obtain the following equation:
$$V \rho a = ma + T\sin \theta \tag{2}$$
Substituting for $T$ using $(1)$ in $(2)$, we get:
$$V \rho a = ma + mg \tan \theta$$
Replacing $m$ with $V \sigma$, we get:
$$V \rho a = V \sigma a + V \sigma g \tan \theta$$
$$\rho a = \sigma a + \sigma g \tan \theta$$
Isolating $\tan \theta$ on one side, we get:
$$\tan \theta = \frac{a}{g} \left(\frac{\rho}{\sigma} - 1\right) \tag{3}$$
$\tan \theta$ is positive if $\theta$ is positive and $\tan \theta$ is negative if $\theta$ is negative in the range $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$.
Refer the diagram and notice that a positive value of $\theta$ indicates that the balloon moves forward and a negative value of $\theta$ indicates that the balloon moves backwards.
The part of the right-hand-side of the equation $(3)$ which decides the sign of $\tan \theta$ is $\left(\frac{\rho}{\sigma} - 1\right)$.
Further analysis will reveal that:
$\tan \theta$ is $-ve$ when $\rho < sigma$
$\tan \theta$ is $0$ when $\rho = \sigma$
$\tan \theta$ is $+ve$ when $\rho > \sigma$
Inference
balloon sways forward
The balloon sways forward when the density of the air filled in the balloon is less than the density of the air. A helium filled balloon will sway forward as it is less dense than the air surrounding it.
balloon does not move
The balloon will not change direction if the density of the air filled in the balloon is equal to the density of the air surrounding it.
balloon sways backward
The balloon will sway backwards if the density of the air filled in the balloon is more than the density of the air surrounding it.
