How much extra distance to an event horizon?

Question

How much extra distance would I have to travel through space to get from Earth to a stellar mass event horizon? (compared to the same point in space without a black hole)

Answer 1

I suspect you're not asking the question you're really interested in, because the answer to your question is really boring. If you jump into a black hole you'll see the event horizon retreating before you, and you'll never cross it. The distance you've travelled is an ambiguous quantity since of course in your frame you're stationary and have travelled no distance at all. The time you take to pass the distance $r=r_s$ then hit the singularity is finite, and for stellar mass black holes very short.

A far more interesting question is if you hover outside the horizon and let down a tape measure how long would it have to be to reach the horizon i.e. what do you get by integrating $dr$ in a radial direction towards the event horizon? The Schwarzschild metric is:

$$ ds^2 = -\left(1-\frac{r_s}{r}\right)dt^2 + \frac{dr^2}{\left(1-\frac{r_s}{r}\right)} + r^2 d\Omega^2 $$

Lets suppose we hover at a distance $r_1$ from the singularity and let down a tape measure to measure the distance to some point at a radial distance of $r_2$. Because $dt$ and $d\Omega$ are constant the equation for the line element simplifies to:

$$ ds = \frac{dr}{\left(1-\frac{r_s}{r}\right)^{1/2}} $$

To get the length of the tape we just need to integrate this expression from $r_1$ to $r_2$:

$$\begin{align} s &= \int_{r_2}^{r_1} \frac{dr}{\left(1-\frac{r_s}{r}\right)^{1/2}} \\ &= \int_{r_2}^{r_1} \frac{r^{1/2}dr}{\left(r-r_s\right)^{1/2}} \end{align}$$

To integrate this we cheat and look up the answer in a GR book, the result being:

$$ s = \left[ z \sqrt{z ^2 - r_s} + r_s \ln \left( z + \sqrt{z ^2 - r_s} \right) \right]_{z_2}^{z_1} $$

where we've used the substitution $r = z^2$ to make the integral manageable.

To make this concrete lets take a black hole with the mass of the Sun, so $r_s$ = 2954m, and we'll start from 5km out i.e. $r_1 = 5000$. Let's graph the length of the tape as a function of $r_2$:

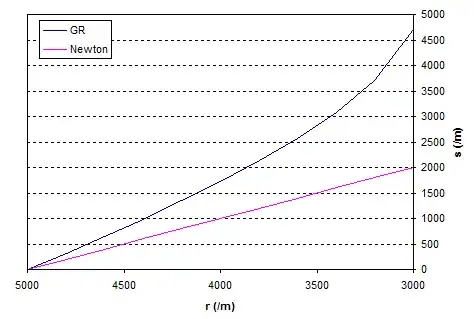
The magenta line is the Newtonian result, i.e. if space was flat, and the blue line is what we actually measure. The tape measure distance from $r = 5km to the event horizon is about 4,780m compared to the Newtonian calculation of 2046m.

So the affect of the curvature is to make the distance measured radially greater than $r_1 - r_2$. However I must emphasise that this is not what you'd measure if I threw you into the black hole. This is the distance measured by an observer hovering far from the event horizon.

Answer 2

The integral John Rennie gave can be upgraded by the gammafactor, assuming the motion of the observer is in the $\rm r$ direction, and the large $\rm R$ is the observer dependend physical distance:

$${\rm \Delta R= \int_{r_2}^{r_1}}=\frac{\sqrt{g_{\rm r r}}}{\gamma} \ \rm dr$$

but you have to check what gammafactor to use for which coordinates. If you are falling into the black hole from rest at infinity or with the negative escape velocity

$$\rm v=-v_{esc}=-c \sqrt{r_s/r}$$

in the classical Schwarzschild/Droste coordinates we have

$$ \sqrt{g_{\rm r r}} = \frac{1}{\sqrt{1-\rm r_s/r}}$$

and the gammafactor for the infalling observer also is

$$ \gamma = \frac{1}{\sqrt{1-\rm v^2/c^2}} = \frac{1}{\sqrt{1-\rm r_s/r}} $$

so the radial expansion and the length contraction cancel out in his frame:

$$ \frac{\sqrt{g_{\rm r r}}}{\gamma} = 1$$

that is why in Gullstrand/Painlevé coordinates where the $\rm -v_{esc}$ is absorbed into the $g_{\rm t r}$ and the local velocity $\rm v$ is not relative to stationary but free falling reference observers (the so called raindrops), and $\rm v=0$ in that coordinates equals $\rm v=-v_{esc}$ in the other coordinates, you get

$$ \sqrt{\bar g_{\rm r r}} = 1$$

and the spatial components of the covariant metric are euclidean, so

Hamilton & Lisle wrote: "In the river model, space itself flows like a river through a flat background"

and the distance is simply $\rm r_2-r_1$. If you are not falling with the escape velocity, the local factor doesn't cancel to $1$ and the distance is different from $\rm r_2-r_1$. If you are slower than the escape velocity it is larger, and if you are faster it is smaller.

Behind the horizon it is the other way around if you take $\rm v$ (relative to the black hole itself) as a measure for how fast you are, but note that $\rm v$ and $\rm dr/d\tau$ are generally different things. The closer to $\rm c$ your $\rm v$ is (from above or below), the more contraction you get. Inside the black hole where you have to have $\rm v>c$, a smaller $\rm v$ (but still larger than $\rm c$) equals larger $\rm dr/d\tau$ than a $\rm v$ much larger than $\rm c$ and $\rm dr/d\tau \to \infty$ equals $\rm v \to c$ outside and inside of the horizon.

In special relativity (where the escape velocity is always $0$ since there's no gravity) the distance for a moving observer would also be shorter than $\rm r_2-r_1$, since when you start moving towards your target, the distance shrinks by the gammafactor of your velocity.