How do we account for unstable real particles using Feynman diagrams ($W$, $Z$ boson)?

Question

I have recently been concerned with the production and detection of $W^{\pm}$ and $Z^0$ bosons. As it is well known, the literature is often unclear about virtual/real particles, so let me premise that I subscribe to the idea that a virtual particle is merely a computational tool arising from the perturbation expansion. Nonetheless, due to such idea, I'm starting to feel dubious about how the particles in the experiments can be real and how computations describe that.

For example, the way I have learned about $SP\overline{P}S$, during $p\overline{p}$ collision quarks interact and a real $W$ boson is produced. $q\overline{q}\to W^{\pm}$. Clearly, this will soon decay and produce e.g. a charged lepton-neutrino pair. Beware, I mean it as a two process step, this is not the usual "story" about virtual particles popping up and disappearing, which would be the tree level of $q\overline{q}\to l\nu$. Up to this point, I had seen no diagrams.

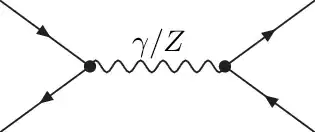
Nonetheless, learning about LEP, I've run into this diagram (actually two diagrams, one for $\gamma$ and the other for $Z$).

It is very clear to me that at $\sqrt{s}=m_{Z_{0}}$, the $Z_0$ channel would dominate, nonetheless, this is a virtual Z. No matter how close it is to being on-shell, this is a virtual particle, not a real particle decaying. The difference is quite relevant as far as I'm concerned: virtual particles are not real particles, unstable particles are. Yet, only this diagram is considered and not the one including the two-step process described above:

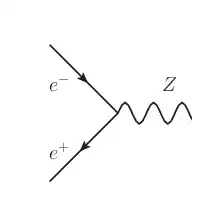
(this would be just the first step) which does not violate energy conservation. This occurs to me as a different contribution, since here $Z_0$ - unstable or not - is real. I can see why having an unstable particle as an external state would be troublesome (although we accept that for decays), yet I can't see how the first diagram, in which $Z_0$ is virtual, could also contain the contribution of the second in which a real $Z_0$ that later decays is created. Why is it so?

I could only find this sentence in this answer by A. Neumaier

This raises the question why virtual particles are often confused with unstable particles, or even identified. The reason, I believe, is that in many cases, the dominant contribution to a scattering cross section exhibiting a resonance comes from the exchange of a corresponding virtual particle in a Feynman diagram suggestive of a collection of world lines describing particle creation and annihilation.

Answer 1

yet I can't see how the first diagram, in which $Z_0$ is virtual, could also contain the contribution of the second in which a real $Z_0$ that later decays is created. Why is it so?

In QM there is a very well defined procedure for calculating transition amplitudes from an initial state $|in\rangle$ to a final state $|out\rangle$: you apply the time evolution operator $U(t)$ to the state $|in\rangle$ and take the inner product $\langle out | U(t) | in \rangle$. In QFT we usually start with a Lagrangian that defines the dynamics and interactions of the fields, and from that obtain the time evolution (e.g. via the path integral). But we only have one Lagrangian - we don't have one Lagrangian for "real" particles and one for "virtual" particles, so there is absolutely no reason we should get two separate contributions as you imagine for a process with the same initial and final states and the same interactions. Indeed, when you do this calculation you get an amplitude that depends on the incoming and outgoing particles' momenta (for states defined in momentum space), e.g. $\mathcal{A}(p_1,p_2,k_1,k_2)$, which has a resonance when the momentum transfer is equal to the mass of the intermediate particle (i.e. it is "on-shell") for processes like those in the question.

Now you can interpret this any way you like. I'm not sure that arguing whether virtual particles are "real" or not has any actually meaning. The physics however is quite clear.