1

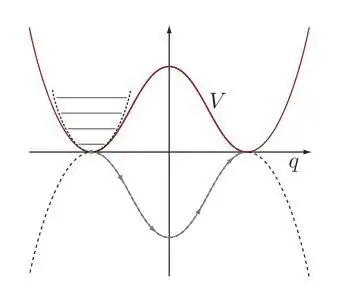
When we talks about quantum mechanical tunneling in the formalism of path integral, we normally say that there's no classical (stationary-phase) path connecting the two minima of the potential so we need to go to the imaginary time formalism.

potential

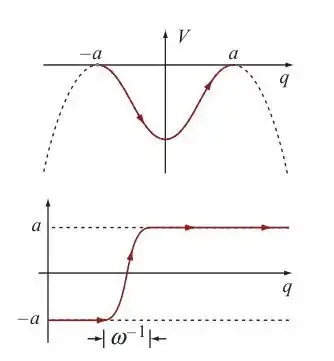
See, for example, the figure in Altland&Simons Chapter 3.3.1, we want to calculate $G(a, -a; t)$ using semi-classical approximation. Mathematically, we just need to find a classical trajectory s.t. $q(0) = -a, q(t) = a$ and expand around it. That's easy, as long as the particle starts at $q(0) = -a$ with sufficient velocity, it can roll over the barrier and get to $q(t) = a$.

But A&S said (chapter 3.3.1):

In doing so, it is understood that the energy range accessible to the particle is well below the potential barrier height......Of course one may think of particles “rolling” over the potential hill. Yet, these are singular and energetically inaccessible by assumption.

I don't understand what they are saying, since mathematically we just want to calculate $G(a, -a; t)$ and it is defined by path integral, it has nothing to do with "energy of the particle".

Similarly, when we use the imaginary time formalism and write the classical trajectory as combination of instantons, we assume that the instanton has no initial velocity at the hill of the potential. (So, the instanton actually last for infinity long time, the classical trajectory written as combination of instantons are just the approximate stationary phase solution.) But again, thinking mathematically, we just want to find a solution s.t. $q(0) = -a, q(\tau) = a$, as long as we give a small velocity for the particle at $\tau = 0$, we can find the exact solution satisfying this condition. (the particle moves slowly down the hill due to the small initial velocity and then goes across the valley and then gets to the other hill.) So why are we expanding the path integral around these multiple approximate stationary-phase solutions not around the unique exact solution?

instanton

Qmechanic
  • 220,844
Jason Chen
  • 647

2 Answers2

1

  1. Well, we know the quantum mechanical path integral $$\langle q_f, t_f | q_i,t_i \rangle ~=~ \int_{q(t_i)=q_i}^{q(t_f)=q_f} \! {\cal D}\frac{q}{\sqrt{\hbar}}~\exp\left(\frac{i}{\hbar} S[q]\right) \tag{1}$$ has an asymptotic semiclassical expansion, cf. the steepest descent/saddle-point/WKB method and e.g. this Phys.SE post.

  2. The caveat is that one may have to perform analytic continuation (AC) into the complex plane.

  3. AC becomes important in the case of quantum tunnelling, where the are no allowed real-valued classical solutions that can carry/support the leading/dominant contributions of the path integral $$\langle q_f, t_f | q_i,t_i \rangle~=~\sum_n \langle q_f, t_f |n \rangle \exp\left(-\frac{i}{\hbar} E_n(t_f\!-\!t_i)\right) \langle n |q_i,t_i \rangle\tag{2}$$ at energies below the barrier threshold.

  4. It turns out that the Wick-rotated Euclidean path integral is particularly useful in organizing the semiclassical expansion. The leading/dominant contributions are given by instantons.

  5. For more details, see e.g. this & this Phys.SE posts.

Qmechanic
  • 220,844
0

Classically, a particle in a potential has energy $$ E=\frac{mv^2}{2} + V(x). $$ Only if this energy exceeds the height of the barrier, $E>E_b$, can the particle pass to the other side. For $E<E_b$ the particle will oscillate near the potential minimum - which one, depends on the initial conditions (i.e., whether $x(0)>0$ or $x(0)<0$). This means that near the minimum of the potential its velocity is not small: $\frac{mv^2}{2}=E_b$.

Of course, in quantum mechanics the particle can tunnel through a barrier, so the solutions localized near one of the potential minima cannot be correct. Sp we need to apply WKB, or path integral, or some other method to account for the tunneling and find the true ground state, or simply numerically.

Quantum mechanically, the energy states are also quantized, so that the whole exercise makes sense only when the ground state energy turns out to be well below the potential barrier - otherwise, we simply conclude that our approach doesn't work, and the results of the (approximate) calculation are incorrect.

See also the discussion of this potential in another context in
What is the reason for power laws appearing at phase transitions?

Roger V.
  • 68,984