2

In QED we have can find a function $$D=f(N_i)\tag{1}$$ where $f(N_i)$ means a function of number $N_i$ of external lines only.

In 4D, we have $$D=4L-P_e-2P_\gamma.\tag{2}$$ This step is universal. We can have a similar expression for any theory, I think.

And then an identity from diagram theory $$L=I-V+1\tag{3}$$ Where $V$ is the number of vertex and $I\equiv P$ the number of internal lines.

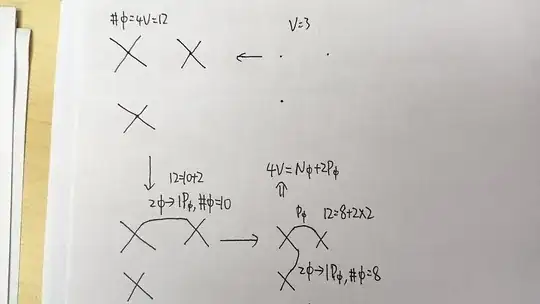
And the lecture by Matthias Neubert claimed:The only vertex of QED connects two fermion lines to a photon line, and hence we can express $$V=2P_\gamma+N_\gamma=\frac1 2(2P_e+N_e).\tag{4}$$

Can someone explain it in detail why this identity is true? And can we find a similar identity for any theory and finally have a function $$D=f(N_i).\tag{5}$$

Qmechanic
  • 220,844
MakiseKurisu
  • 534

2 Answers2

5

  1. OP's sought-for general eqs. (1) & (5) for the superficial degree of (UV) divergence $D$ do not exist. Additional information about the actual interactions in the theory is implicitly needed. A formula of the form $$ D~=~d - \sum_f [\phi_f] \underbrace{E_f}_{\equiv N_f} - \sum_i [\lambda_i] V_i$$ is possibly the closest that one can get to what OP is asking for, cf. the second-last formula in eq. (1) of my Phys.SE answer here .

  2. OP's eq. (2) follows more or less directly from the very definition of $D$, namely by counting powers of loop momentum variables (i.e. $-1$ for each internal fermion propagator and $-2$ for each internal boson propagator), cf. the 2nd line in eq. (1) of my Phys.SE answer here.

  3. OP's eq. (3) is explained around eq. (8) of my Phys.SE answer here.

  4. OP's eq. (4) holds because QED only contains a 3-valent $\gamma e\bar{e}$-interaction vertex. It follows because (for each particle species) there is a bijective map between the legs of vertices and the available propagator ends (i.e. 2 for each internal propagator and and 1 for each external propagator).

  5. See also e.g. this related Phys.SE post.

Qmechanic
  • 220,844
1

This is a supplementary explanation of Qmechanic's point 4. I want to add a comment but I think it's better to draw a picture to show what I mean.

Let's begin with an easier version: $\phi^4$ theory in 4D with $V=3$ 4-valent vertices, cf. figure. QED is spiritually the same.

example

Suppose we have $V$ vertices, then we have $4V$ $\phi$ in total. When we want to create a propagator, we stick 2$\phi$. And others become external legs.

So we have the following relations: $$D=4L-2P$$ $$P=L-V+1$$ $$4V=N+2P$$

Then for $\phi^4$ theory in 4D we finally have $$D=4-N.$$

However, for $\phi^3$ theory in 4D, the relation $$4V=N+2P$$ will be replaced by $$3V=N+2P$$ but other 2 remain the same! So we cant have an expression like $$D=4-N,$$ which is (1) in my question!

Also, if we have different type of interactions, things will become much more complicated.

Qmechanic
  • 220,844
MakiseKurisu
  • 534