Light travel distance and comoving distance in the Big Crunch scenario

Question

I'm aware that the Big Crunch is practically ruled out, but I need it to ask my question. Imagine, that we live at the cosmic time of the reversal of the expansion, precisely when it stops. At the time of this "cosmic event" the universe is seemingly static. Would it result with the equal light travel distance and the comoving distance at our cosmic time when the expansion stops before it reverses? My reasoning behind the equality of these distances is that the static universe metric is Minkowski metric. Why would these distances differ in this metric?

Answer 1

Co-moving distance is defined as the proper distance between two objects at the same epoch (usually defined to be now). Clearly if that were the definition then the answer to your question is no, since the co-moving distance doesn't change (due to expansion/contraction at least).

However, I think you are asking - what if we defined the co-moving distance to be the proper distance at some future epoch when a decelerating universe becomes (instantaneously) static? Would that distance be equal to the light travel time distance?

i.e. Does $$ c \int_0^{z} \frac{dz'}{H(z')} = c \int_0^{z} \frac{dz'}{(1+z')H(z')}\ ?$$ The answer would seem to be no.

The light travel time is not determined by some instantaneous condition, it depends on history too. To clarify, $H(z)$ depends on the values of the cosmological energy densities as a function of redshift and therefore lookback time.

Answer 2

kurac wrote: "Imagine, that we live at the cosmic time of the reversal of the expansion, precisely when it stops."

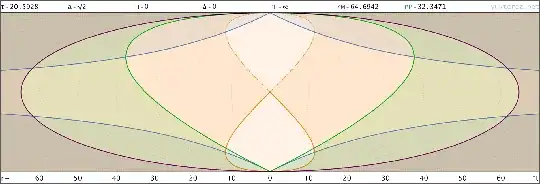
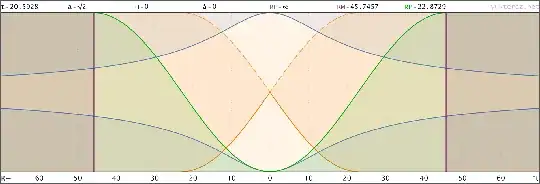
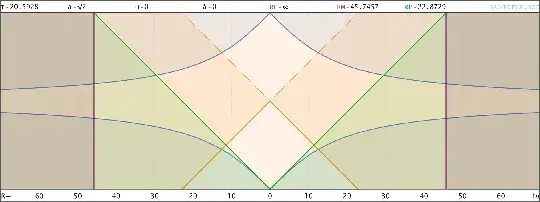
This is the spacetime diagram of such a big crunch universe in proper, comoving and conformal coordinates, the lightcone originates at the turning point where H=0:

Hubble radius: blue, particle horizon: green, light cone: orange, comoving worldlines: gray, half circumference (maximum separation distance): purple.

kurac asked: "Would it result with the equal light travel distance and the comoving distance at our cosmic time when the expansion stops before it reverses?"

You must mean the proper distance, since the comoving distance depends on when you set your a to 1. In the big crunch scenario the moment where the two match is infinitesimally short, but if you take a universe that stays static like we did in in answer 838358, the future light cone stays 45° in proper distance coordinates after the universe became static.

In comoving distances it's also 45° if you define the scale factor as 1 at its maximum, but that's a free choice. It will stay a straight worldline though, but in the big crunch scenario it's only straight in the immidiate vicinity of the observer and starts bending as time goes back or forth.

kurac wrote: "this means, that the relation between the cosmic redshift and the redshift/recession velocity vrs≡cz is no longer valid"

That was never valid, this is only a valid approximation for minimal redshifts.

kurac wrote: "My reasoning behind the equality of these distances is that the static universe metric is Minkowski metric."

Neither is the universe you described static, since even when H=0 that does not mean dH/dt=0, nor do we have Minkowski just because it is static. A static universe needs not only H=0 but also dⁿH/dtⁿ=0, see here.

kurac asked: "What will happen with the redshift of the light from the distant sources that we receive when the expansion stops?"

Since the scalefactor was smaller when the light was emitted than it is when the light is received at the turning point there will be the corresponding redshift.

If the light was emitted when the scalefactor was larger there will be blueshift. The factor by which the frequency differs is the same factor by which the scalefactor differs between sending and receiving since 1+z=1/a.

If you live x years after the turnaround time the light from a galaxy that travelled 2x years from the galaxy to you will have no redshift since the scalefactor x years after the turnaround time is the same as the scalefactor x years before the turnaround time, but that's a special case.