6

I need to clarify a detail about the particles horizon (also called the causality horizon, not to be confused with the event horizon). For simplicity, consider an euclidian static universe, with a sudden beginning at $t_{\circ} = 0$ (the "Big Bang" of that model), and a brutal ending at $t = t_{\bullet}$ (the "Big Crunch" of the model). The cosmological scale factor is constant : $a(t) = 1$ for $t_{\circ} < t < t_{\bullet}$. (think of that model as a 3D "game-universe" that you launch at some time on your computer, then quit after a while. Poor virtual creatures living in the game !)

Here's a picture I made to represent that simple universe. Distance $\mathcal{D}$ is the proper distance from the stationary observer, shown as a blue vertical word-line on the picture. The red vertical line is the world-line of a stationary particle. $\mathcal{H}_{\mathcal{E}}$ is the event horizon of the observer, while the past light-cone $\mathcal{H}_{\mathcal{C}}$ is the causality (or particles) horizon at time $t_0$ (the present of the observer). $\mathcal{A}$ and $\mathcal{B}$ are two arbitrary events.

game-universe

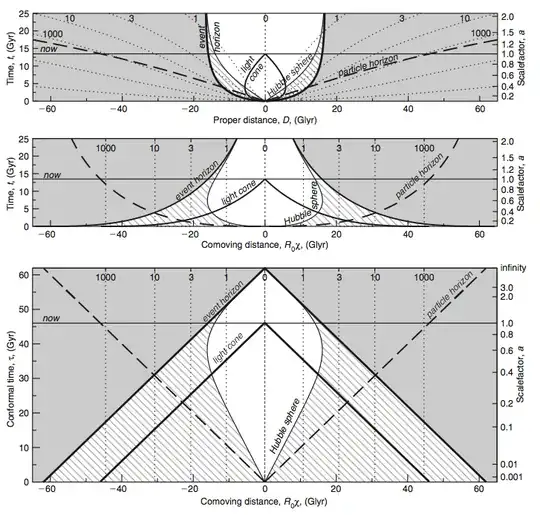
Now, what confuses me are the (very nice) pictures shown in the answer there : Is the cosmic horizon related to the Big Bang event?. I'm showing the pictures from that answer here for reference : horizon diagram

On these pictures, the particles horizon is depicted as an inverted (future-oriented) large cone, not as an evolving smaller (past-oriented) light-cone. Why ?

If I add this inverted light-cone on my picture above, event $\mathcal{A}$ would be outside that particles horizon. Yet it is an observable event for a time $t > t_0$ (as shown with the green dashed line).

I believe that the particles horizon shown on these pictures isn't right and should be labeled as something like "particles horizon distance" instead (not "particle horizon"). Am I wrong ?

EDIT : A variation of the first picture, with a better representation of the particle horizon (? I'm not convinced yet !) : game-universe 2

Community
  • 1
Cham
  • 8,015

1 Answers1

1

"Event A is outside the particle horizon" means by definition that at the time $t(\mathcal{A})$, no event of its world-line for $t \leq t(\mathcal{A})$ can be seen by the stationary observer at time $t(\mathcal{A})$, which agrees with your figure ($\mathcal{A}$ is to far from the observer on the time interval $[t_o \ t(\mathcal{A})]$). Similarly, in your picture, event $\mathcal{B}$ is inside the particle horizon because at $t = t(\mathcal{B})$, the stationary observer is able to see one point of the world-line of $\mathcal{B}$ that occurred for some $t \leq t(\mathcal{B})$. Hence there is nothing contradictory. Besides, your suggestion to label the "particle horizon" as something like "particles horizon distance" makes sense, as by definition (taken from your reference question), the "particle horizon" is "the distance - at that time - to the furthest object that can be seen". And to answer your initial question, the cone in the figures is correct, the distance to the furthest object that can be seen is necessarily increasing with the time (the more you wait, the more distant are the objects you can see).