Measuring voltage drop from induced current

Question

I'm having trouble connecting voltage drops and induced current. Imagine you have a triangular loop make up off three resistors. You place this loop in a constantly changing magnetic field. This changing magnetic field will cause an EMF and a resulting induced current in the loop.

Now imagine I place a voltmeter across one of the resistors. What does the voltmeter read? $IR$ or $2IR$? If you look at the situation one way, you are measuring the voltage drop across one resistor, so $V$ would equal $IR$. But if you look at in another way, you're also measuring the voltage drop across the other half of the circuit which contains two resistors (hence a voltage drop of $2IR$).

I have tried to model this situation in my schools physics lab and I do see that there is a voltage drop across the resistor so the answer is not "there is no voltage drop". My model wasn't perfect, but it seemed to imply that the voltmeter read $3IR$? How could that be?

Answer 1

Once you add a changing magnetic field, the electric field no longer is conservative -- i.e. there is no longer a consistent definition of voltage!

A voltmeter measures $\int_a^b \mathbf{E} \cdot d\mathbf{s}$ along a path from $a$ to $b$. Normally this value doesn't depend on the path, so you can speak of "the" voltage drop between $a$ and $b$. In this situation, the value does depend on the path -- you can get $IR$ or $2IR$ or any other value depending on how you set up the wires of the voltmeter. For example, if you wound the voltmeter leads around the triangle several times, you might get $25IR$.

Answer 2

I would try to explain without involving mathematics!

What we are talking about here is an induced electric field, as work done along different paths for such a field is different, there is no definition of potential difference! This directly implies that you cannot measure any sort of potential difference you hoped to measure!

The emf is not even supposed to be same across both 1resistor and 2 resistor's series; All there is supposed to be is an induced emf which generates a current in accordance with lenz laws.

Furthermore I believe you seemed to think that your experiment gave results for $ I×3R $ because the loop of voltmeter would have started circulating its own current giving a larger value than what you expected to observe!

I would propose the following experiment to get the value of induced emf: 1. Place an idealistic ammeter in the circuit to measure current in the circuit 2. Find the net resistance of the circuit, for 3 resistora combined as you said it would be treated as parallel of $R$ and $2R$ 3. Now you may use basic ohms law to find the induced emf.

Since the exact reverse of this method is what we use to calculate current in the circuit, the above method should give satisfactory results!

Answer 3

What the voltmeter reads in this case is not the classical voltage drop as the concept of voltage itself, as a scalar function whose gradient gives the field, becomes redundant. What it displays is, indirectly, the current through it, which in the case of induced emfs, is not related to "potential drop" across its end. (it will display $V$ as its reading where $V=Ir$, $I$ the current through it, and $r$ the resistance of the voltmeter.

As an example, consider the case you present in the question. Three resistors of resistances $R=5$ each are connected to form a triangle. A voltmeter of resistance $r=100$ is connected across two vertices. Let the change in magnetic flux be confined to the triangular portion only, and be $1 weber/s$. Therefore, the line integral of the field along a line which completely includes the area with changing magnetic flux must be $1 volt$. Let the current through the voltmeter be $I_1$(from A to C) and across the two resistors (except the one across which the voltmeter is attached) be $I$(clockwise). The current through the resistance across which the voltmeter is connected is $I-I_1$(from A to C).

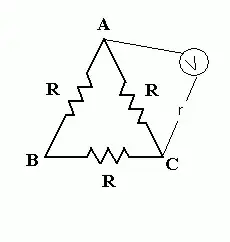First, consider, the line integral along the triangular portion in clockwise manner. The integral will give $$-2IR-(I-I_1)R=1$$ $$-15I+5I_1=1$$ Considering the line integral along $C\rightarrow B\rightarrow A\rightarrow \text{Voltmeter}\rightarrow C$ clockwise, we get $$-2IR-I_1r=1$$, since in both the case the change in magnetic flux (time rate of change) is same, as the change is confined to the triangular area which is bound completely by both the line integrals. $$-10I-100I_1=1$$ on solving we get $I=21/310=0.068$(anticlockwise) and $I_1=1/310=0.0032$(anticlockwise). Therefore the voltmeter will show $I_1r=0.32V$ which is equal to $(I-I_1)R$ but not $2IR$ since, in cosidering the voltmeter attached to only the resistance $AC$, we get a simple circuit without any changing magnetic flux, but considering the voltmeter as being attached to the resistances $CB$and $BA$, we get a circuit which has a changing magnetic flux, which needs to be accounted for, and hence reading will not be according to $2IR$, or the hypothetical "potential drop" across the two resistors.