It affects and it does not in different cases
Case 1: When contact area do not affects the frictional force
You know that frictional force $f$ is $$f = N*\mu$$ where $\mu$ is the frictional coefficient of the surface and $N$ is the normal force acting on the surface. Now look at the image below
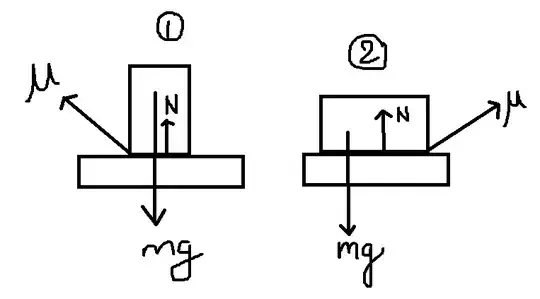
both the blocks have same mass in $fig(1)$ and $fig(2)$ but the contact area is different let the block 1 have the are $Am^2$ and block 2 have the are $2Am^2$, in the both the images there is equal frictional coefficient that is $\mu$
Now force exerted by the first block per square meter is $$N_1 =\frac{mg}{Am^2}$$and the force exerted by the second block is $$N_2 = \frac{mg}{2Am^2}$$so since both the blocks have same frictional coefficient $\mu$ so frictional force between block 1 and the bottom plank is$$f_1 = N_1*\mu*a_1$$ here $a_1$ is the area of the contact between the blocks, so$$f_1=\frac{mg}{Am^2}*\mu*Am^2\implies mg\mu$$ and the contact force between block 2 and bottom plank is$$f_2 = N_2*\mu*a_2$$ here $a_2$ is the area of the contact between the blocks, so$$f_2=\frac{mg}{2Am^2}*\mu*2Am^2\implies mg\mu$$$$\implies f_1=f_2$$ so you see here there is no effect of contact area on the frictional force.
Case 2:When contact area do affects the frictional force
i don't if this is a correct example or not but here is goes
take example of books kept in shelf standing vertically side by side and are tightly packed so if you will try to remove a big book with a greater surface are you will have to apply more force as compared to in removing smaller books with smaller surface area
Hope you got it
