I was reading an article by Lev Vaidman, who helped create the quantum bomb tester thought experiment which inspired much work on quantum interaction-free measurements (IFMs), that was analyzing the exact meaning of interaction pertaining to IFMs. I am a little cautious to accept his exact words on the matter since he is proudly convinced of the many-worlds interpretation and, although I have no problems with people subscribing to any interpretation, I want to know that I'm learning from an unbiased source. In this article, Vaidman claims that quantum IFMs as produced in Kwiat et al. are interaction-free in the sense that a photon or other quantum object is not located at the location of the measured object, but not in the sense that there is no exchange of energy or momentum. How can this be? How interaction-free are quantum IFMs? I know many of the specifications rely on one's interpretation, but I just want to know if the quantum is located at the site of the measured object and if there is an energy exchange between the measured object and the quantum that "measures" it and, if so, how.
2 Answers
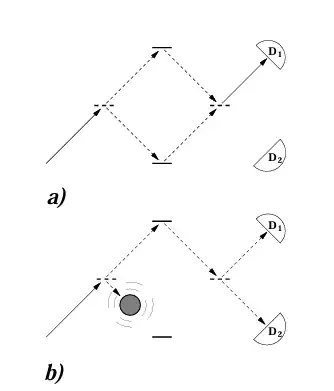
The setup considered in the original paper is simple enough such that the questions asked in the post are readily answered by reviewing it. The first part (a) of the image below (taken from the same paper), shows the configuration of an interferometer when no "measured object" is present. In this case, there is an interference between the two possible paths taken by a photon, so the photon always reaches the detector $D_1$ (The interferometer is tuned such that two paths leading to $D_2$ interfere destructively).
In the second case (b) an object (bomb in this case) blocks one of the paths, thus there is no interference and the photon can reach either $D_1$ or $D_2$ with equal probabilities.
We can think of the second case in the following way: at the first beam splitter, the photon has a 50% probability of moving forward and a 50% probability of moving towards the bomb (and thus exploding it). If the photon moves forward, it then has a 50% probability of hitting either $D_1$ or $D_2$ (thus 25% overall probability for each detector). If the photon is measured by $D_2$, we know that something was blocking one of the paths.
It is clear from the above description, that when the photon is detected by either $D_1$ or $D_2$, there is no energy or momentum transfer between it and the bomb (any such transfer would have necessarily caused the bomb to explode). This is independent of interpretation: in the MWI language we would say that we happen to live in the world where the photon took the upper path; in the language of collapse we would say that the presence of the bomb (which effectively measures the location of the photon after the first beam splitter) collapsed the wave function to the same path. Either way the photon in this case does not reach the bomb or interacts with it.
It is also worth noting that detecting the photon at $D_2$ does not tell us anything about the nature of the object blocking the path, such as whether it is a bomb or any other object. It only tells us that something was blocking the path.
- 2,680
- 1
- 6
- 15
The IFM experiment involves single photon interference. That is, producing a laser beam in the interferometer so that the probability that two photons are in the interferometer at the same time is negligible. I will suppose that we're dealing with a standard Mach Zehnder interferometer with two arms for the sake of illustration. When a photon goes through an interferometer the probability of it coming out of each port is dependent on what would happen to a photon going along both of the possible paths through the interferometer: quantum interference.
In an interferometer with nothing in either arm the probability is dependent on the difference between the lengths of the arms. You can adjust the interferometer and position detectors $D_1$ and $D_2$ so that the photon interacting with a particular point on the final beamsplitter has a probability of 1 of going toward $D_1$ and 0 of going toward $D_2$.
If you then place an opaque obstruction in one of the arms the probabilities change to 1/2 for each detector. So if you detect the photon at $D_2$ then there is an obstruction. If you make the obstruction another detector $D_o$ you would find that $D_o$ doesn't detect a photon when $D_2$ detects a photon and vice versa. So there is a photon at $D_2$ or the obstacle but not both.
A photon carries a momentum of $\hbar k$ so a photon carrying that momentum went into the interferometer and a photon with the same momentum was detected coming out of the interferometer. So in the case where you successfully detect the obstacle you will not find that any momentum was transferred to the obstacle.
However, the expectation value of the momentum at the ports of the interferometer is 1/2 of what it would have been without the obstacle and the expectation value of the photon momentum at the obstacle comprises the other 1/2. So when the photon is absorbed a momentum of $\hbar k$ is absorbed by the obstacle. In such cases the obstacle isn't detected by the interferometer. So momentum is exchanged with the obstacle only in situations in which the obstacle isn't detected.
There is a dispute about what is happening in reality to explain the results of quantum experiments. This dispute is said to be about the interpretation of quantum theory. The equations of motion of quantum theory, if taken seriously as a description of reality, say that there are two versions of the photon, one in each arm and the obstacle blocks one of those versions. In such a theory every object you see exists in multiple versions and on the macroscopic scale those versions are sorted approximately into layers each of which approximately obeys classical equations of motion, this is often called the many worlds interpretation:
https://arxiv.org/abs/1111.2189
https://arxiv.org/abs/quant-ph/0104033
The MWI is what you get if you work out the implications of the equations of motion of quantum theory as you would for any other physical theory.
Other explanations of what is happening in reality in quantum experiments may say something else. For example, the pilot wave theory claims that the world is made of particles and that the wave function is some sort of mathematical artefact to describe the statistics of those particles. This requires modifying quantum theory and that modification may be experimentally testable:
https://arxiv.org/abs/2409.01294
In pilot wave theory the unoccupied states can affect what happens to the occupied states:
https://arxiv.org/abs/quant-ph/0312227
This seems like an excuse for evading the MWI explanation to me but YMMV.
Some physicists have tried to modify quantum theory to eliminate the other versions of macroscopic systems: collapse theories. These theories also may produce different predictions than those of unmodified quantum theory. For a review see
https://arxiv.org/abs/2310.14969
I haven't found a clear account of what's happening in an interference experiment in collapse theories. Pilot wave and collapse theories don't currently reproduce most of the predictions of quantum theory:
https://arxiv.org/abs/2205.00568
If you want to try to understand what such theories say about IFM you may have to invent such an explanation yourself.
- 11,359
- 1
- 16
- 33