There is a derivation of centripetal acceleration in uniform circular motion which uses an isosceles triangle as shown in the following diagram:
My question now follows:
The direction of the centripetal acceleration derives from the direction of $\Delta \mathbf{v}$, which is part of an isosceles triangle, not a right triangle. Shouldn't the direction of centripetal acceleration then be close to 90 degrees but not exactly 90 degrees to the velocity?
I suppose the derivation that you are referring to is set up in a similar way to that shown below:
If this is the case it is necessary to understand that the quantities such as $\Delta s$, $\Delta \theta$ and $\Delta \mathbf{v}$ are, in the limit, infinitesimally small. Therefore in this limit - as these aforementioned quantities approach zero - the vector $\Delta \mathbf{v}$ makes an angle ever closer to 90 degrees with both $\mathbf{v}_1$ and $\mathbf{v}_2$.
Another way of visualising this is to imagine that two long arms $\mathbf{v}_1$ and $\mathbf{v}_2$ of the isosceles triangle are closing together like a pair of scissors as $\Delta \theta$ approaches zero. Therefore they are becoming more and more nearly parallel and thus $\Delta \mathbf{v}$ is more and more nearly perpendicular to $\mathbf{v}_1$ and $\mathbf{v}_2$.
Therefore the acceleration will not be 90 degrees to the velocity during the process of taking the limit. It will only be perpendicular in the limit. However, the definition of acceleration is the limit. So therefore the acceleration is exactly perpendicular to the velocity.
Filling in some information about limits from Nathan's answer (+1).
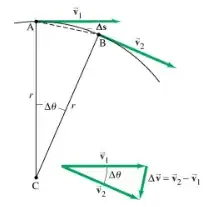
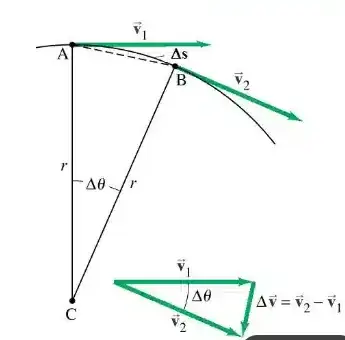
In the diagram, you calculate the centripetal acceleration by using the velocities at A and B. This tells you about the rate of change in velocity over the interval. But you want to know the rate at which velocity is changing at one point somewhere in the interval. All the other points have velocities that are a little bit different. So the answer you get is an approximation.
$$a_{centripetal} \approx \frac{v_B - v_A}{t_B-t_A}$$
You can make it a better approximation by using a smaller interval. How good can you get? Can you get a perfect answer with absolutely no error (assuming perfectly uniform circular motion)?
You can. You look at smaller and smaller intervals that give better and better approximations. You figure out what number the approximations are headed to, and that is the perfect answer.
We can do this for the angle at the base of the isosceles triangle.
Every triangle you look at has an angle $<90^o$. Are the approximate angles headed to $91^o$? No. None of them get as big as $90.5^o$, so they never get to $91^o$. You can apply the same argument to eliminate every number bigger than $90^o$.
Likewise you might ask if they are headed to $89^o$? No. You can pick a slimmer triangle where the angle is $89.5^o$. The approximations go past $89^o$. Again, you can apply a similar argument to eliminate every number $<90^o$.
The only number you can't eliminate is $90^o$.
It would be nice if you could just use a "triangle" with $90^o$ angles. But if you try, A and B are the same point. You wind up with
$$a_{centripetal} = \frac{v_B - v_B}{t_B - t_B} = \frac{0}{0}$$
Taking a series of approximations is forced on you. A derivative handles this for you. It tells you the answer to where are the approximations $\frac{v_B - v_A}{t_B-t_A}$ headed?
To understand the situation in the limit required by the definition of acceleration, it is probably better to use analytic formulas instead of pictures.
The following time dependence of coordinates can describe a uniform circular motion (center at the origin of the coordinates): $$ \begin{align} x(t) &= R \cos( \omega t)\\ y(t) &= R \sin( \omega t).\tag{1} \end{align} $$ The resulting components of the velocity are: $$ \begin{align} v_x(t) &= -R \omega \sin( \omega t)\\ v_y(t) &= ~~R \omega\cos( \omega t). \end{align} $$ Let's consider the average acceleration between time $t$ and time $t+\Delta t$: $$ \begin{align} a^{(m)}_x(t,\Delta t) &= -R \omega \frac{\left[ \sin( \omega (t+\Delta t)) - \sin( \omega t) \right]}{\Delta t}\\ a^{(m)}_y(t,\Delta t) &= ~~R \omega \frac{ \left[ \cos( \omega (t+\Delta t)) - \cos( \omega t) \right]}{\Delta t}.\tag{2} \end{align} $$ For any finite $\Delta t$, it is evident that the terms in the square brackets of equations $(2)$ are not proportional to $\cos(\omega t)$ and $\sin(\omega t)$ respectively. If this would be the case, the direction of the average acceleration would coincide with the radial direction. What we find if we use a Taylor expansion around $t$ of the function evaluated at $t+\Delta t)$, (including the second order in $\Delta t$) is: $$ \begin{align} \frac{\left[ \sin( \omega (t+\Delta t)) - \sin( \omega t) \right]}{\Delta t} &=\omega \cos (\omega t)+ O(\Delta t)\\ \frac{ \left[ \cos( \omega (t+\Delta t)) - \cos( \omega t) \right]}{\Delta t}&=-\omega \sin(\omega t)+O(\Delta t).\tag{3} \end{align} $$
Therefore, although for any finite $\Delta t$, the direction of the average acceleration is not radial, in the limit $\Delta t \rightarrow 0$, necessary to find the instantaneous acceleration, it becomes radial.
A more intuitive picture, also from the geometric point of view, can be obtained by noticing that for every differentiable function $f$: $$ \frac{{\mathrm d}f}{{\mathrm d}t} = \lim_{\Delta t \rightarrow 0} \frac{f(t+\Delta t) - f(t)}{\Delta t} = \lim_{\Delta t \rightarrow 0} \frac{f(t+\Delta t) - f(t-\Delta t)}{2 \Delta t}. \tag{4} $$ Using the second limit in formula ($4$), the so-called symmetric finite difference approximation to the derivative, the analytic value of the average acceleration and the geometric construction shows an average acceleration with a radial direction, even for finite values of $\Delta t$, due to the exact cancelation by the symmetry of the terms with the wrong trigonometric function. Indeed, $$ \begin{align} \frac{\left[ \sin( \omega (t+\Delta t)) - \sin( \omega (t-\Delta t)) \right]}{\Delta t} &=\cos (\omega t) \frac{\sin(\omega \Delta t)}{\Delta t}\\ \frac{ \left[ \cos( \omega (t+\Delta t)) - \cos( \omega (t-\Delta t)) \right]}{\Delta t}&=-\sin (\omega t) \frac{\sin(\omega \Delta t)}{\Delta t}\tag{3} \end{align} $$ for every $\Delta t$ has the radial direction at each time $t$.
In the case of the symmetric finite difference formula, the triangle made by the three vectors ${\bf v}(t+\Delta t)$, ${\bf v}(t-\Delta t)$ and the difference ${\bf v}(t+\Delta t)-{\bf v}(t-\Delta t)$ is again an isosceles triangle, but in this case, neither of the two equal sides coincides with the velocity at the time $t$ and the vector difference is parallel to the radial vector at the time $t$.
