Why the normal vector addition does not seem to work in centripetal acceleration?

Question

It is known that centripetal acceleration acts at an angle of 90 degrees to the tangential velocity. This acceleration vector then causes an increment $\mathbf{a} \Delta t$ to be added to the original tangential velocity. This vector addition triangle is a right-angled triangle.

The question then follows: Since the vector addition triangle is a right-angle triangle, and we know in a right-angled triangle the resultant velocity's direction and magnitude will change. So then why does the speed remain constant in centripetal acceleration?

Answer 1

Its important to note that the velocity is infact not constant,as it is changing its direction.

But,I'm going to show you why the speed is constant if we have the fact that the angle between the force vector and the velocity vector is 90° everytime.

The angle between the vectors being 90° is just saying;

$$ \vec{F} \cdot d\vec{v} = 0$$

$$\implies \vec{F} \cdot \frac{d\vec{s}}{dt} = 0$$

$$\implies \vec{F} \cdot d\vec{s} = 0$$

$$\implies W = 0$$

$$\implies \Delta KE = 0$$

$$\implies |\vec{v}| = \text{constant}$$

So, if the angle between the velocity and force vector is 90° throughout, the object in its new path of motion will have a constant speed.

Answer 2

The concern raised in this question, as I understand it, is that we start with a tangential velocity:

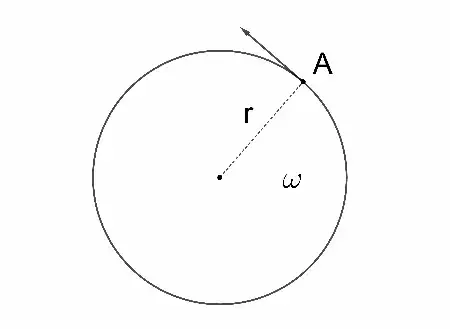
But then, the acceleration, being perpendicular to the velocity, causes the increment $\mathbf{a} \Delta t$ (the blue vector in the diagram) of velocity to be added, thus forming a right angled triangle of vector addition:

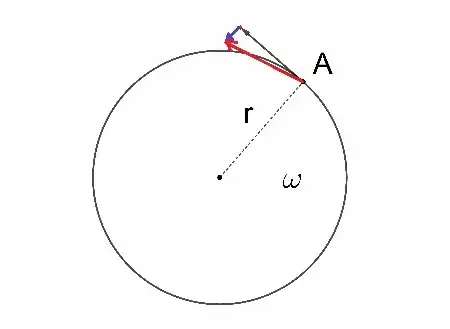
This being the case, the concern raised is due to Pythagoras' theorem; the new velocity vector seems to be longer.

Proper formal proofs (or the argument via work in another answer) can sidestep these problems but in this answer I am attempting to allay the concerns raised about this pictorial/visual argument. Perhaps the best way to do this is to visualise the following situation:

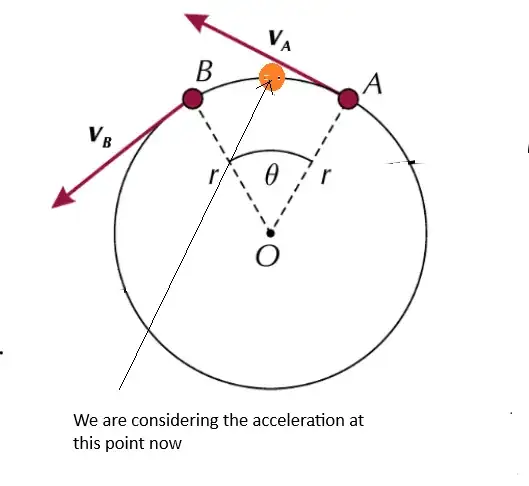
We see in the diagram above that for the moment under consideration, the starting velocity is $\mathbf{v}_A$ and the ending velocity is $\mathbf{v}_B$. Now consider the average acceleration during this short interval. Well, being the average it seems intuitively reasonable to imagine this acceleration being concentrated at the point exactly between point A and point B. Now we have an isosceles triangle instead of a right angled triangle and so the velocity vector does not change its magnitude.

Final comment: Of course, when limits are taken it doesn't matter whether we consider the right triangle or this isosceles triangle. Nevertheless, from an intuitive point of view, hopefully the original poster may find this second visual argument a little more convincing.

Answer 3

Speed but not velocity is constant. The velocity vector changes all the time exactly due to the acceleration component.

Answer 4

You cannot add acceleration and velocity by vector addition because they are quantities of different dimension. You cannot add m/s and m/s$^2$.

What you can add is velocity and the product of acceleration and an infinitesimal time interval:

$$\vec v + \vec a~dt$$

And if you perform this addition for uniform circular motion you will have adjusted the direction of the velocity vector by an amount $d \vec \theta $, which is the amount it would change over a short time $dt$ to follow the circular path.

Answer 5

If the curve is given in parametric polar coordinates (r(t),θ(t)) , the velocity and acceleration vectors can be calculated in the moving base . (We denote by a point the derivation with respect to the parameter t) :

$\vec{r}=r\vec{u}$

$\frac{d\vec{r}}{dt}=\frac{dr}{dt}\vec{u}+r\frac{d\vec{u}}{dt}=\frac{dr}{dt}\vec{u}+r\frac{d\vec{u}}{d\theta}\frac{d\theta}{dt}$

$ \vec {V}=\dot {r}\vec {u}+r\dot {\theta }\vec {v}$

in the same way we find that the acceleration

$ \vec {A}=\frac{d\vec{V}}{dt}=(\ddot {r}-r\dot {\theta }^{2})\vec {u}+(r\ddot {\theta }+2\dot {r}\dot {\theta })\vec {v}$

if: $\;\;r=cst\;,\;\dot{\theta}=cst\;\;$==> $\vec {V}=r\dot {\theta }\vec {v}$

$\frac{d\vec{V}}{dt}=-r\dot {\theta }^{2}\vec {u}\;\;$i.e.

$\;\;d\vec{V}=\vec{A}\,dt\,=-r\dot {\theta }^{2}dt\,\vec {u}=-\frac{ {V }^{2}}{r}dt\,\vec {u}$

the variation of the $\vec{V}$ is on the axis with direction vector $\vec{u}\perp \vec{V}$ .