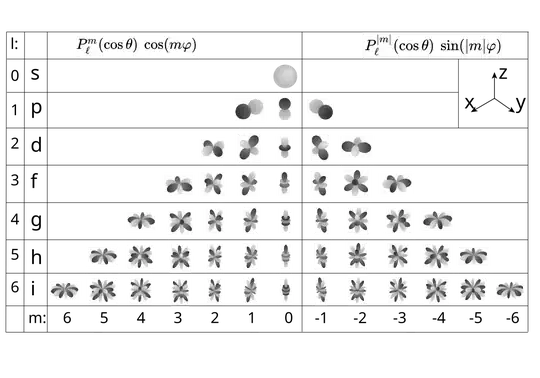
Below is an image of real spherical harmonics in wikipedia.
These are used in different scenarios, but when they represent charge distributions on a spherical shell (see e.g. this awesome answer), then from top to bottom, the successive rows lead to monopole, dipole, quadruple, octopole, ... terms in the spherical multipole expansion. Better yet, unlike the heuristic point-charge poles in Cartesian coordinates, each of these mutipole spherical distributions never produces any residual higher multipole terms 1. These are pure multipoles.
For me, this should be the origin of the $n$-pole naming. Because you really can count at most 1, 2, 4, 8 "poles" (or rather protrusions) in the charge configurations in the rows $s,p,d,f$. However this correspondence stops at octopole. For the hexadecapole, or 16-pole, you count in the $g$ row. But the most "poles" you get is 12 poles for the $m=3$ charge configuration.
So, where should I count to find 16 "poles" for multipole expansion?
1: For example, a pair of $+/-$ point charges placed at $±z$ is our textbook dipole, but in this configuration they have nonvanishing octopole electrostatic potential and other higher-pole potentials.