-1

this question is a variation of the one posted here. In which the answer seems to be "Bob always sees the same pattern regardless of whether the which-way information is erased by Alice". This seems to be the same answer given here, here, here, and here.

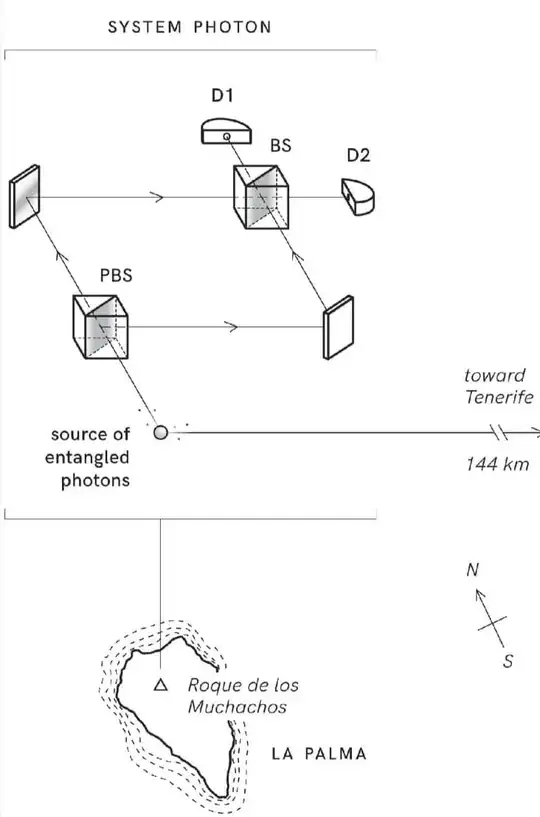
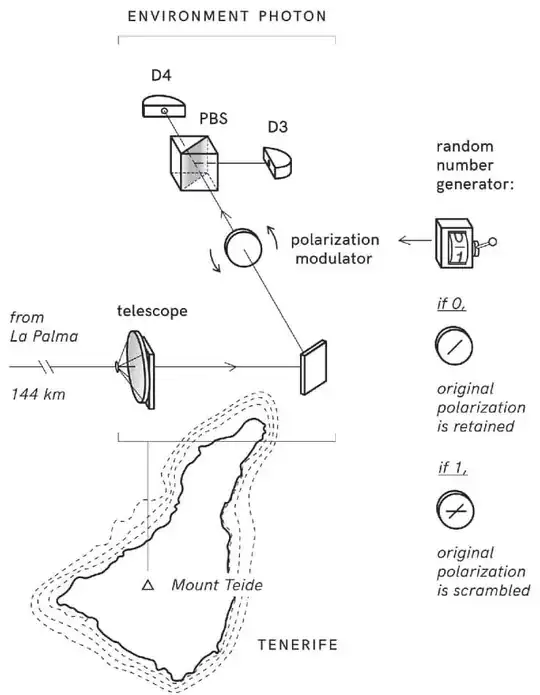
Reading Through Two Doors at Once (chapter To Erase or Not To Erase) one of the experiments described is a similar one led by Zeilinger (I believe this is the experiment, although it doesn't seem to be exactly as the one described in the book). This experiment is described here starting by "In their test, Zeilinger & co. used entangled photons ...". These two images summerize Bob's (La Palma) and Alice's (Tenerife) setup.

Bob - La Palma: Bob - La Palma

Alice - Tenerife: Alice - Tenerife

In this case, Bob has a Mach–Zehnder interferometer. Alice has a random number generator. When 0 is generated, the original polarization is retained, and the corresponding system photons arrive at D1 or D2 (in Bob's Mach–Zehnder interferometer) in equal numbers. However when 1 is generated, the original polarization is scrambled (the which-way information of the environment photon is erased). In this case - according to the book - all the system photons end up in D1, and none in D2 (in Bob's Mach–Zehnder interferometer).

With this setup, one could think that if Alice always erases the which-way information, all the system photons end up in D1. And if Alice never erases the which-way information, the system photons would arrive in equal numbers at D1 and D2. Thus allowing FTL (faster than light) communications:

  • Alice and Bob are in different galaxies, millions of light-years apart.
  • Every minute, Bob generates 1M photon pairs, measures how many land in D1, and how many in D2. They are all ending up in D1, none in D2.
  • Alice changes from always -> never.
  • In the "next" 1M photon pair generation, Bob realizes they go in equal numbers to D1 and D2, instead of all of them to D1.
  • Alice didn't need to wait millions of years to convey this information, just one minute.

So I guess regardless of whether Alice erases the which-way information, half the system photons arrive at D1 and half arrive at D2 (is this correct, the number of photons that arrive to D1 and D2 doesn't depend on what Alice is "tempering" with, right?). But how is this consistent with the experiment described in Through Two Doors at Once? Assuming the random number generator returns half of the times 0, and half of the times 1, and assuming there are 1M photon pairs:

  • For the photons the random number generator returned 0 -> 250k arrived to D1, and 250k arrived to D2.
  • For the photons the random number generator returned 1 -> 100% arrived to D1.

So the number of photons that arrived to D1 is strictly larger than the number of photons that arrived to D2.

jmarhuen
  • 23

2 Answers2

2

@DrChinese is actually an expert in this field, so I'll defer to his answer when he responds. In the meantime, though, having looked at the original paper I believe the book misrepresents the experiment in a crucial way: Bob always detects equal numbers of photons at D1 and D2, regardless of Alice's settings. What changes is the correlation between Alice's and Bob's photons. That is, if you consider only the photons that Bob detects when Alice's detector D3 is triggered, then in one case all of Bob's photons are at D1, and in the other they are split evenly between D1 and D2. This correlation can be discovered only if you know both Alice's and Bob's results, i.e. only if they exchange the information using ordinary (slower than light) communication.

It's still an interesting experiment for a number of reasons, but it's not nearly as spooky as some popular science books describe.

Sabine Hossenfelder has an overview of delayed choice experiments here which takes a bit of the mystery out of it. As with any popsci account take it with a grain of salt, but I think in this case she does a good job.

Eric Smith
  • 11,450
2

This is another great experiment in the arsenal of the Zeilinger teams. They have been exploring as many variations on what is usually called "quantum nonlocality". Many of there demonstrate, in various permutations, what happens when changes are made to the experimental setup while entangled photons are in midflight from the source to the various detectors.

In this one, a choice is made to switch from a which-way (a/k/a which-path or welcher-weg, or sometimes particle-like) test to an interference (wave-like) test based on an random independent/remote decision. According to quantum theory, the ORDER of the execution of the different components - Alice's measurement, Bob's measurement, and the decision on the type of test to perform - is irrelevant to the results. They refer to this point as demonstrating "causally disconnected" outcomes (choice).

Critically: Regardless of whether the choice of test is particle-like or wave-like, there is ALWAYS two-fold detection. Either D1 or D2 fires for Bob (in La Palma with the interferometer), and either D3 or D4 fires for Alice in Tenerife. So why is there no way to send a message? After all, you can look at Fig. 5 and see obvious differences between the A and C graphs. Two critical points here.

i) The graphs A and C are based coincidences between Alice's detectors (D3/D4) and Bob's (D1/D2). To obtain this information, a classical signal is used to bring the results of Alice and Bob together in a common location after the runs are completed. So clearly, no opportunity for FTL signaling if you need a classical signal to distinguish the A pattern from the C pattern.

ii) But what about the fact that an MZI - along - sends all of its photons to a single detector? That's the main premise of the question, right? The answer is that this is not your usual MZI as you might picture it. Instead of a Beam Splitter (BS) as the first element of Bob's apparatus, there is a Polarizing Beam Splitter (PBS). This is an important distinction in the setup. Without trying to explain the ins and outs of why they did this (it's explained in the paper), the simple fact is that the D1 and D2 detectors ALWAYS fire at nearly exactly equal 50-50 chance. That is regardless of which type of test is being performed.

Of course, this is pretty much an exact re-statement of what Eric Smith has said in his answer. :)

DrChinese
  • 2,593