This is mainly meant as a more concise and more general formulation of the problems and realizations occurring to me while thinking about the apparatus I described in this question. The main problem with the apparatus described there, was that it used the assumption, of it being possible to align 2 wave packets with basically no overlap into 1 ray and by doing that removing the (almost) orthogonality using a unitary transformation, which can’t be possible by definition of the unitarity of a transformation. My conclusion was that it has to be impossible to align 2 spatially strongly separated wave package-states by unitary time evolution, because that would change the scalar product. However that is exactly, what is done in a for example a Mach-Zehnder-experiment. Therefore the question formulated in the title arised in my head.
1 Answers
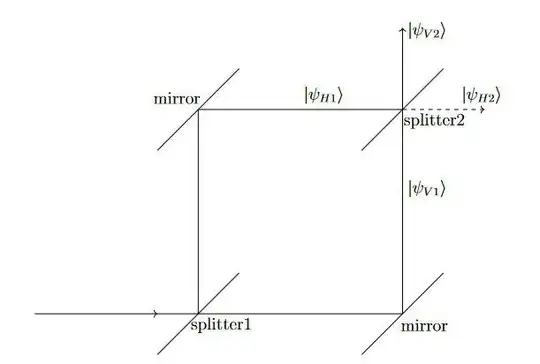
To track down the emergence of the described contradiction, I tried to imagine the time development of a wave a package in a Mach-Zehnder-interferrometer.
I will in this case focus on the action of the second beamsplitter, though the one of the first one would work analogous with opposite time direction. So we start with a particle in a superposition state of 2 spatially distinct wave packages with a $\pi$-phase difference $|\psi_1\rangle = \frac{1}{\sqrt{2}} \left(e^{i\pi} |\psi_{H1}\rangle + |\psi_{V1}\rangle\right)$, where the indexes $H1$ and $V1$ are associating the state with the direction (horizontally or vertically), it enters the beamsplitter with. Now let $\hat{U}$ be the operator propagating the packages from the starting time to some time after they passed the beamsplitter and let $|\psi_{H2}\rangle$ and $|\psi_{V2}\rangle$ denote the states of the wave packages leaving the splitter in horizontal or vertical direction after that time. Looking at the action of such time development, we get: $\hat{U} |\psi_{H1}\rangle = \frac{1}{\sqrt{2}} \left(|\psi_{H2}\rangle + e^{i\pi} |\psi_{V2}\rangle\right)$ and $\hat{U} |\psi_{V1}\rangle = \frac{1}{\sqrt{2}} \left(|\psi_{H2}\rangle + |\psi_{V2}\rangle\right)$. Note that in the expression it is taken into account, that the beamsplitter will apply a $\pi$-phase shift on reflection on the optical more dense medium, but no phase shift on transmission or reflection on the optically less dense medium.
Now if we look at the state after passing through the mirror we get: $$|\psi_2\rangle = \hat{U} |\psi_1\rangle = \frac{1}{\sqrt{2}} \left(e^{i\pi} \hat{U} |\psi_{H1}\rangle + \hat{U} |\psi_{V1}\rangle\right) = \\\ \frac{1}{\sqrt{2}} \left(\frac{1}{\sqrt{2}} \left(e^{i \pi}|\psi_{H2}\rangle + e^{i 2 \pi} |\psi_{V2}\rangle\right) + \frac{1}{\sqrt{2}} \left(|\psi_{H2}\rangle\right) + |\psi_{V2}\rangle\right) = |\psi_{V2}\rangle.$$ So the 2 initially spatial distinct wave packages will indeed leave the construction as single wave package.
Now lets check the overlap integrals: $$0 \approx \langle\psi_{H1}|\psi_{V1}\rangle =^? \langle\psi_{H1}|\hat{U}^\dagger \hat{U} |\psi_{V1}\rangle = \left(\hat{U} |\psi_{H1}\rangle\right)^\dagger \hat{U} |\psi_{V1}\rangle = \left(\frac{1}{\sqrt{2}} \left(|\psi_{H2}\rangle + e^{i\pi} |\psi_{V2}\rangle\right)\right)^\dagger \frac{1}{\sqrt{2}} \left(|\psi_{H2}\rangle + |\psi_{V2}\rangle\right)$$
Since $|\psi_{H2}\rangle$ and $|\psi_{V2}\rangle$ are also spatially strongly distinct so almost orthogonal it follows:
$$\left(\frac{1}{\sqrt{2}} \left(|\psi_{H2}\rangle + e^{i\pi} |\psi_{V2}\rangle\right)\right)^\dagger \frac{1}{\sqrt{2}} \left(|\psi_{H2}\rangle + |\psi_{V2}\rangle\right) \approx \frac{1}{2} \langle\psi_{H2}|\psi_{H2}\rangle + e^{i\pi}\langle\psi_{V2}|\psi_{V2}\rangle = 1 - 1 = 0$$ So the overlap integral remain $\approx 0$ under the propagation through the beamsplitter. Note though, that for this to be true it is important to include the parts of the wavefunctions, where their superposition cancels out, in the calculation. In the case of the alignment to 1 ray one would get a contribution to the overlap integral from the 2 rays leaving the construction with constructive interference, that is oppositely signed but equal in absolute value compared to the contribution to the overlap integral of the 2 ray interfering destructively.
This means the answer to the question is: A transformation aligning 2 distinct wave packages into 1 does not lead to a direct contradiction with the unitary of that transformation the way one (or rather I) would intuitively think it might. However this does not mean that we can change the overlap integral of 2 states by such transformation, while maintaining its unitarity.
- 1,395