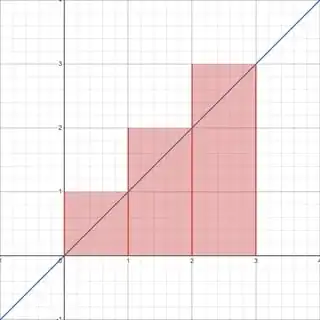
I started learning 1D kinematics and learnt definitions of constant velocity and constant acceleration. I thought that if a particle is changing its velocity uniformly then it has constant acceleration. From this I tried to plot x-t graph from the varying velocity. If a particle is moving with acceleration of $1 \,\text{m}/\text{s}^2$, then its velocity for first second would be $1 \,\text{m}/\text{s}$, $2 \,\text{m}/\text{s}$ for second second, $3 \,\text{m}/\text{s}$ for third and so on. Then I thought that since the particle is moving with $1 \,\text{m}/\text{s}$ at first second, it would have displaced $1 \,\text{m}$ and in second second, as its velocity was $2 \,\text{m}/\text{s}$ so it covered additional $2 \,\text{m}/\text{s}$ and so on an extra meter for each second than previous. In total, its displacement was $1 \,\text{m}+2 \,\text{m}+3 \,\text{m}$ that is $6 \,\text{m}$ of displacement. But actually the real displacement was $4.5 \,\text{m}$. How am I wrong?
4 Answers
The (signed) area under the velocity-time graph, shaded in red, is the displacement.
What you think is happening:
What actually happens:
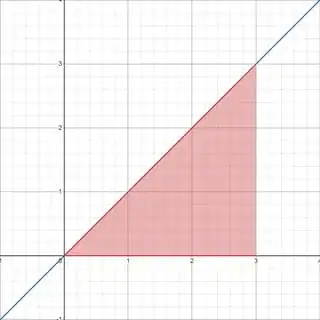
So the reason is that the velocity is changing continuously and not in steps. However, if you take smaller and smaller steps, your result approaches the true result, which is an integral.
- 15,416
To travel 1 meter in 1 second, an object needs to travel at an average speed of $1 \,\text{m}/\text{s}$. But an object accelerating from rest at $1 \,\text{m}/\text{s}^2$ does not have an average speed of $1 \,\text{m}/\text{s}$ over the first second, it has a top speed of $1 \,\text{m}/\text{s}$ - at all times before the first second is over, the object is moving slower than $1 \,\text{m}/\text{s}$. The object can't move slower than $1 \,\text{m}/\text{s}$ for the entire first second, yet find that it's moved $1 \,\text{m}$ in that second.
Over the first second, the object has an average speed of only $0.5 \,\text{m}/\text{s}$ (for constant linear acceleration, the average speed is simply the average of the initial and final speed). Over the second second, it has an average speed of $1.5 \,\text{m}/\text{s}$. Over the third second, it has an average speed of $2.5 \,\text{m}/\text{s}$. The overall average speed for the entire 3 seconds is $1.5 \,\text{m}/\text{s}$ (again the simple average of the final speed of $3 \,\text{m}/\text{s}$ and the initial speed of $0 \,\text{m}/\text{s}$) , yielding a total distance of $4.5 \,\text{m}$.
- 10,705
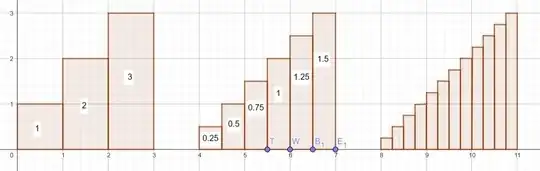
There is nothing special about an interval of one second. $1 \ \mathrm{m/ s^{2}}$ does not literally mean a increase of $1 \ \mathrm{m/s}$ every second as in the first chart below. The real meaning is better approximated by an increase of $1/2 \ \mathrm{m/s}$ every $1/2$ second as in the second chart, or even better by an increase of $1/4 \ \mathrm{m/s}$ every $1/4$ second as in the third chart and so on.
A real object experiencing constant acceleration does not increase its velocity in discrete time steps, but continuously. Since distance is the product of velocity and time, the total distance travelled is the sum of the areas of the strips. The total distance travelled in the first chart is $6$. In the middle chart, the strip areas total to $5.25$. In the third chart the areas total to $4.5625$ and we are getting close to the exact solution already. If you keep doing this process of halving the intervals indefinitely, the total of the infinitesimal strips approaches the correct solution of $4.5$ in the limit. The calculus method of integration does this summation of the infinitesimal strips automatically for you, even if the acceleration is changing, so it is worth learning.
See it is just all about average velocity. The velocity increases from $0$ to $1 \ \mathrm{m/s}$ in $1$ second, that is what acceleration of $1 \ \mathrm{m/s^2}$ means. So in that one second, the velocity is not $1 \ \mathrm{m/s}$ at all points. On average it will be $0.5 \ \mathrm{m/s}$. In $0.1$ seconds, it will be $0.1 \ \mathrm{m/s}$. It gives the velocity at the instant and not over a time interval of $1$ second which I guess you are thinking it like.