You are completely confused regarding the concept of smooth change. This is why we need calculus in basic education.
Your table of values correspond to this following velocity-time graph. The vertical / ordinate / $y$-axis is the velocity in feet per second, plotted against the horizontal / abscissa / $x$-axis of time in seconds.
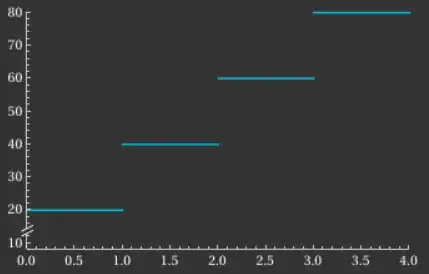
As you can see, you have these ridiculous sudden jumps in velocity every second.
Instead, what we mean with rolling a ball down a smooth slope is that the velocity-time graph looks like
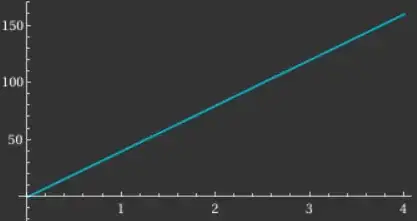
Luckily, for small speeds, the rolling of a ball down a smooth straight slope happens to be well-described by such a graph. This is the case where we give the name of "acceleration is constant", which in maths symbols, is $a=\text{const}$
When acceleration is constant, we can use the $suvat$ equations. In these equations, the initial velocity $u$ is always something you need to know and provide into the problem. It is just some constant that you must start with. Here, your $u=0$. What you called the distance $d$ is upgraded to displacement $s$. There is a small difference: distance always increases, whereas displacement can go negative. When you move forward and then backwards, the distance will keep increasing even when the backward motion cancels out the forward motion, whereas displacement will decrease when cancellation happens. Displacement gives a better correspondence with "where you are".
With the assumption that $a=\text{const}$, you can obtain the $suvat$ equations below:
$$
\begin{align}
v &=u+at \tag{without \(s\)}\\
s &=ut+\frac12at^2\tag{without \(v\)}\\
v^2&=u^2+2as \tag{without \(t\)}\\
s &=\frac{u+v}2t \tag{without \(a\)}
\end {align}
$$
These equations are ordered in a combination of decreasing ease of memorisation and frequency of use. They are all trivial consequences of $a=\text{const}$ so that you can derive all of them from this one fact, but if you want to practice algebra, you just need any two of them and you can derive the rest by simple substitution. The easiest example is to substitute Equation (without $s$) into Equation (without $a$) and obtain Equation (without $v$).
Note that in all of these, while $u=\text{const}$ and $a=\text{const}$, the only way that $s$ and $v$ would make sense, is that they are functions of time, i.e. $s=s(t)$ and $v=v(t)$. The way to mathematically write down mean velocity, which is written as $\left<v\right>$ or as $\bar v$, is
$$\left<v\right>=\frac{u+v}2 \tag{defining mean velocity}$$
which in your case, reduces to
$$\left<v\right>=\frac{0+v}2=\frac v2\tag1$$
and you should be able to notice from the Equation (without $a$) that
$$s=\left<v\right>t \tag2$$
which you might be more familiar when rendered as
$$\left<v\right>=\frac st\tag3$$
With these, you should be empowered to clear every doubt that you might have on this topic.
Instantaneous displacement or position, that we call $s=s(t)$ is a geometrical entity. Calculus supplies the definition for instantaneous velocity, which is our $v=v(t)$, with the definition $v\equiv\dfrac{\mathrm ds}{\mathrm dt}$ and the instantaneous acceleration as $a\equiv\dfrac{\mathrm dv}{\mathrm dt}$, which holds even when $a\neq\text{const}$. Calculus is just unavoidable when you have to deal with continuously changing entities, and there are so many of them in real life.

