Motion formula gives correct answer but without formula gives wrong answer

Question

Assume a body with initial velocity= 10 ms final velocity= 20 ms and acceleration= 2 ms , so the time to reach final velocity will be 5 seconds. If we try to find distance it will travel in 5 seconds starting with initial velocity we get:

$$S = ut + \dfrac{1}{2} at^2$$ Putting in the values we get answer 75 m

Also using this formula S = average velocity* time = 15 * 5 = 75 m

Everything is ok but when we try to find distance using a table we get this:

Time [s]	Velocity [m/s]
0.0	10
1.0	12
2.0	14
3.0	16
4.0	18
5.0	20

Adding all velocities we get answer 90 m

I don't get this, why 90?, is something wrong with table?

Answer 1

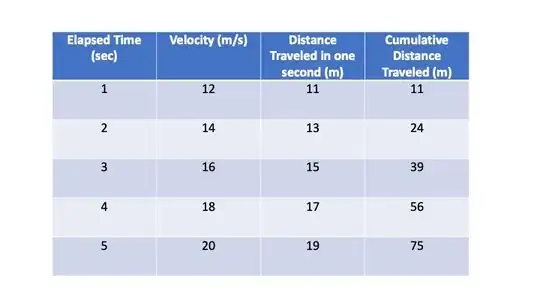
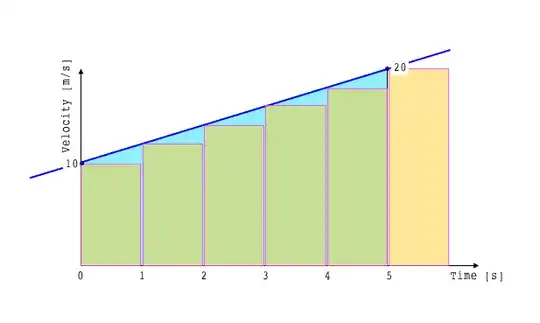
You stepped into the magical wonderland of numerical integration. Basically, you want to estimate the area under the line $v=v_0+at$, or the integral of $v$ from 0 to 5. You chose a timestep of $\Delta t=1$ and this is quite large for numerical integration. By choosing a smaller timestep you will get closer to the true answer. Note that if you choose a timestep that is not one, you have to multiply each contribution in the sum by $\Delta t$.

More importantly, with a large timestep getting things exactly right is harder. You made the simple mistake of including the endpoint in the sum. Let's see why that matters. Take a look at the graph below. Here you want to estimate the area under the red line and the area in blue is what you actually calculated. As you can see, the rectangle between $t=5$ and $t=6$ is a gross overestimation of the area, and it should not be included. If we exclude it, we get 70. This is already much closer!

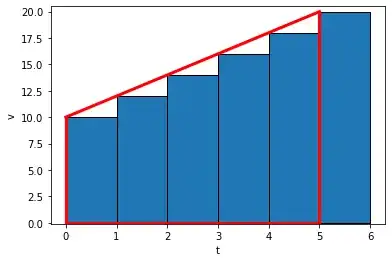
But we can do better. There is a more accurate way of numerical integration, called trapezoidal integration. Instead of summing little rectangles, we sum trapezoids. See the image below. Because we have a straight line, this will give the exact answer (can you reason why?). The area of a trapezoid is given by $\tfrac 1 2(a+b)w$ where $a$ is the left edge, $b$ is the right edge and $w$ is the width. The integration now looks as follows

\begin{align} \text{area }=&\,\tfrac 1 2(v_0+v_1)\Delta t+\tfrac 1 2(v_1+v_2)\Delta t+\tfrac 1 2(v_2+v_3)\Delta t\\ &+\tfrac 1 2(v_3+v_4)\Delta t+\tfrac 1 2(v_4+v_5)\Delta t\\ =&\,\Delta t(\tfrac 1 2 v_0+v_1+v_2+v_3+v_4+\tfrac 1 2 v_5) \end{align}

Plugging in your values (with $\Delta t=1$) gives \begin{align} \tfrac 1 2 \times 10+12+14+16+18+\tfrac 1 2 \times 20=75 \end{align}

So using trapezoidal integration, we arrive at the right answer. But note that this happened because we integrated a straight line. If we integrated a parabola or something more complicated, we would still be off. But by reducing the timestep you can get as close as you want.

Image from Khan academy

Answer 2

There's nothing wrong with the table actually the thing is this table doesn't give the full picture. We should keep in mind that between t=0 and t=1 second (basically the first second) the velocity doesn't remain constant and keeps changing due to the fact it is accelerating even in the first second for example at t=0.1s the velocity doesn't remain 10 m/s but it changes to 10.2 m/s so you cannot just add the velocities for each second and expect to get the right answer. Instead what you can do with this table is deduce that the average velocity is (10+12+14+16+18+20)/6,which would be beautifully 15 m/s and you can obtain the distance travelled to be 15m/s * 5s which is 75m.

Answer 3

Even though the above answer already gives you the desired result I think there is still something to expand on. The fundamental mistake you are making is that you are overcounting the number of points in your table. Your table has 6 entries even though there are only 5 seconds of travel. So adding up the entries will actually give you a result that looks close to that of traveling 6 seconds under the constant acceleration (though the result you got would be off by 1 due to the averaging mentioned in the other answer).

What you are essentially doing with adding the values of the table is describing a problem where from $ t = 0$ to $t = 1$ the velocity is $10m/s$, from $t = 1$ to $t = 2$ it is $ 12 m/s$ and so on including the last entry which gives a velocity of $20 m/s$ for the interval $t = 5 $ to $ t = 6$. So you add an extra interval to your calculation.

So how could we modify the approach you took? Firstly we obviously need to get rid of the last interval so our time only runs to $5$ not $6$. The second modification we need is that the velocity in the interval $[t,t+1]$ would not be the velocity at the start of the interval but rather the average velocity in that interval. Since your acceleration is constant this can be calculated by $(v(t) + v(t+1))/2$. Building a table out of this we get

Timeinterval	averagevelocity
[0,1]	11
[1,2]	13
[2,3]	15
[3,4]	17
[4,5]	19

Taking a sum of all of these values does indeed give the correct result.

Answer 4

The times shown in the table are elapsed times. Then the table fills in as shown below.

Hope this helps.

Answer 5

As @AccidentalTaylorExpandsion explained, you are looking for the blue area under the curve below

But by just adding the values, you got the total yellow area above. The two problems here, is that you are counting the last row for the total distance traveled. So your are overcounting for distance that would be traveled after 5 seconds.

Also and each arbitrary time step assumes constant velocity throughout the step, and as a result you are undercounting for the little blue triangles above each bar.