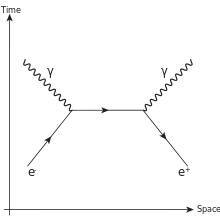
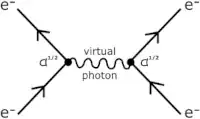
This is a great question, which every student of QFT should be asking themselves at one point or another. I'm surprised to see it's been sitting here for over a year with no good answers yet.
I'll start by debunking each of the key claims in the 2 existing answers:
1a. real particles are defined to be real because they are the observables
This is more of a tautology than an explanation of why we typically only observe on-shell particles
1b. virtual particles aren't observable because their 4-momentum is conserved at every vertex
Incorrect. Energy & momentum are conserved for all particles at every interaction. That's always true, whether they are real or virtual, observable or unobservable.
2a. observing virtual particles would require "virtual eyes" which can scan the false vacuum for fluctuations (joking )
Well, at least this one is humorous... and self-aware about it not being a serious answer!
2b. real particles are free to travel long distances, while virtual particles are only intermediate carriers
This is the most common pseudo-explanation I've seen given in pop science books. It makes sense superficially--but on closer inspection, the argument falls apart. If distance were what mattered, then in order for it to be impossible to observe a virtual particle, there would need to be a hard upper limit on the maximum distance a virtual particle can travel, a hard lower limit on the minimum distance that's observable, and a gap in between rather than an overlap. However, none of those 3 conditions are actually true. Because electromagnetism is a long-range force, virtual photons can travel arbitrarily long distances. In principle, there are virtual photons being exchanged all the time between every pair of charged particles in the universe--even between two electrons in different galaxies! Also, the claim that "we can see free particles but not particles in bound states" falls apart when you realize there are images of individual electrons in atoms (ie, in a bound state) online that you can view but NO images of virtual particles available anywhere, since virtual particles are unobservable.
In addition to those two official answers, there are also the 4 proposed explanations in the original question. Most of these are closer to the truth IMO than anything in the official answers, but none of them quite succeed in fully explaining what's going on. They each capture a part of what's going on but don't really get to the heart of the matter.
I feel like I never fully understood virtual particles until I took a step back and tried to understand the more general concept of virtual states. Virtual particles are harder to wrap our brains around because they show up in the context of quantum field theory, but virtual states show up in ordinary single-particle quantum mechanics and you can ask most of the same questions about them. More specifically, you can ask: what makes a quantum state "virtual" rather than "real", and why isn't it possible to observe a particle in a virtual state?
One example of virtual states is quantum tunneling. According to the classical equations of motion, the total energy of an electron is the sum of its kinetic and potential energies ($T(p^2) + V(x) = E$). Since its kinetic energy T is always positive, there may be classically inaccessible regions of space where $V(x) > E$. A quantum state within one of these regions is called a virtual state because the electron lacks the required energy to be confined to that region.
In one sense, the state is just as "real" as any other state: it's a valid state in the Hilbert space, which corresponds to a single real eigenvalue of a physical observable--for example, a position eigenstate within the forbidden region is an eigenstate of the observable X with a real eigenvalue x. But given the present energy it has, there's no way it could actually occupy that state. It's not that the state itself is fundamentally unphysical or unobservable--it's just that given the initial conditions of that particular experiment it doesn't have enough energy to get into that state.
Nevertheless, quantum tunneling tells us that there is some probability you'll find the electron on the other side of an energy barrier from where it started. How did it pass through the supposedly impenetrable barrier? If we imagine the electron as a classical particle, we'd visualize it moving locally through the forbidden zone (energy barrier) from one virtual state to the next in order to eventually reach the other side. But that's not how quantum tunneling works--it never actually occupies any of those intermediate states on its journey. Instead, it gets there because it has wavelike powers where it isn't restricted to existing at a single spatial location at once. (In more technical terms, energy eigenstates with energy eigenvalue E = $\langle V(x)\rangle + \langle T(p^2)\rangle$ where the spacial extent of its wavefunction includes both sides as well as the forbidden region are perfectly accessible. Those states can be decomposed into a sum of position eigenstates where $V(x) > E$ within the forbidden region and $V(x) < E$ outside.
We can do a mathematical calculation to estimate the probability of the electron tunneling through the barrier by summing together different local paths the electron could have taken through the forbidden zone. But it never actually takes any of those paths. What it does is something more similar to taking all paths at once. But because they are all part of the same coherent superposition they interfere with each other making it incorrect to say "it took this path OR this other path") Any single state along the way would be impossible for it to be in, but it's not impossible for it to be in a superposition of many different inaccessible states. Because once you add those states up... they add up to something that's accessible. It's only when you're looking at one part of a sum and ignoring the rest that things don't make sense--considering the entire sum holistically gives you a more clear idea of what can or can't happen.
With virtual particles, it's largely the same way. Every virtual particle is a valid quantum state in the Hilbert space, corresponding to a specific configuration of quantum fields. There's no reason in principle why you couldn't observe the quantum fields being in a state like that (although it would have to be a fairly different kind of observation from the ones we're used to making with particle detectors designed to measure the location and/or energy of particles interacting with them). But if you start with real particles and end with real particles, the scattering process that gets you there in between is a sum of many different virtual states none of which is ever actually occupied.
So are virtual particles just as "real"/observable as real particles? Not in the experiments these states are traditionally used to describe, since they are never actually occupied. The states themselves would be observable under some conditions, but if we were doing that sort of experiment it's debatable whether even calling them "virtual particles" would be correct since in that situation they would be real occupied states rather than virtual states.
ADDENDUM
I just noticed this comment of yours, which I think is spot on:
Part of me wonders if I'm confusing myself by conflating "off shell" and virtual here? Im not sure if these two notions are entirely equivalent since all non-free particles are necessarily off shell?
The confusion is not necessarily on your part, the term "virtual particle" is used in different ways by different people and is always somewhat in flux. There are at least a handful of different inequivalent but overlapping things people mean when they say "virtual particle".
If we reserve the term "virtual particle" to strictly mean intermediate lines in Feynman diagrams, then yes--this is different from an off-shell particle. Those lines don't represent anything that actually happens in real life... they're not observable since they are at best possibilities rather than actual events that happen, but even as possibilities they are only a partial approximation. Off-shell particles on the other hand, you could produce by other means which have nothing to do with Feynman diagrams or perturbation theory. Off-shell photons are simply the quantum equivalent of near-field excitations of electromagnetic fields. These are physically real fluctuations of the electromagnetic field, they're just somewhat difficult to observe since they're typically very short-lived.
Ultimately, the term "virtual particle" is vague enough that it has caused an enormous amount of confusion, even within academic literature but especially within pop physics & science education/news. On the one hand, people are told that virtual particles are "not real, just a mathematical trick" but on the other hand, they are told that when virtual particle pairs are produced near the event horizon of a black hole, one can accidentally escape and then "becomes real" as Hawking radiation. That's a terrible way of explaining what is already a confusing enough phenomenon. The better way to say it is that what looks like an off-shell photon in one reference frame can look like an on-shell photon in another reference frame. Because time is observer dependent that makes the definition of an "on-shell particle" observer dependent.