It is common to read that the lifetime of a virtual particle is given by the uncertainty relation: $$\tau \sim \frac{\hbar}{E}$$ on the premise that the virtual particle 'borrows energy'. This statement is in fact wrong (at least I think it is) since energy is conserved in Feynman diagrams and thus no energy needs to be borrowed. Given this, how do we actually determine the lifetime of a virtual particle, and why is it not just the same as the real particle?
Asked
Active
Viewed 1,788 times
2 Answers
4
Virtual particles are defined only within the mathematical framework of Feynman diagram calculations for measurable quantities, as crossections and lifetimes.
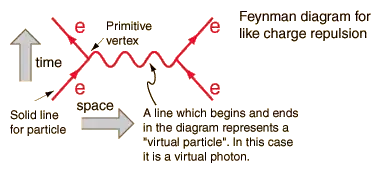
This is the first order in an expansion to get the crossection of e-e- scattering.
The wavy line represents a mathematical term which is under an integral, it is called a photon because it has the quantum numbers of a photon but not the mass, the mass is off mass shell. Have a look at this lecture where the propagator representing mathematically the virtual line, has the mass of the named particle in the denominator, but the four vector describing within the integral the virtual particle is off mass shell.
It is all under an integration and not real. Real on mass shell particles are the incoming and out going dark lines. So there is no lifetime for individual virtual lines. Only for the total interaction a lifetime can be calculated.
anna v
- 236,935
1
That relation you quote has noting to do with borrowing energy. It is just Heisenberg's uncertainty principle. However, in my humble opinion, it is best not to ascribe any "reality" to virtual particles. They are just pictorial representations of terms called propagators which appear when performing perturbation theory on a Quantum Field Theory. There is very little understanding to get along the route you took in your question.