5

The radial Schrodinger equation for the hydrogen atom is given by: $$\frac{1}{R}\frac{d}{dr}\left[r^2 \frac{dR}{dr}\right]+\frac{2m_e}{\hbar^2}\left(Er^2+ke^2r\right)=l(l+1).$$ Following the Bohr model we substitute the energy $E$ and radius $a_0$ given by $$E = -\frac{(ke^2)^2 m_e}{2\hbar^2 n^2},$$ $$a_0 = \frac{\hbar^2}{k e^2 m_e}.$$ We also change variable $r \rightarrow a_0\ r$ to give the following dimensionless radial equation: $$r^2 R''+2rR'-\frac{r^2R}{n^2}+2rR-l(l+1)=0.$$ The standard hydrogen groundstate is $n=1$ and $l=0$.

Instead we try $n=1/2$ and $l=0$.

WolframAlpha gives a solution of the form: $$R(r)=e^{-2r}\ U(\frac{1}{2},2,4r),$$ where $U(a,b,x)$ is the confluent hypergeometric function of the second kind.

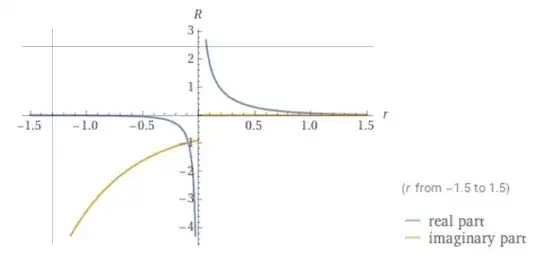
The wavefunction $R(r)$ is badly behaved at $r=0$ with the real part diverging and a discontinuity in the imaginary part. Radial Wavefunction

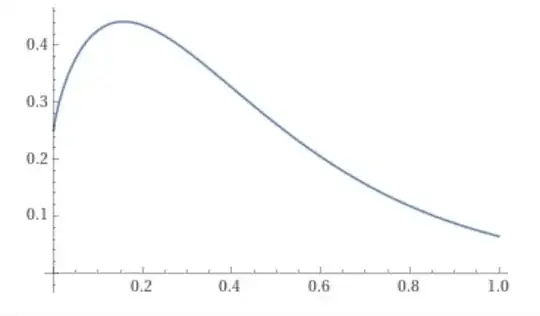
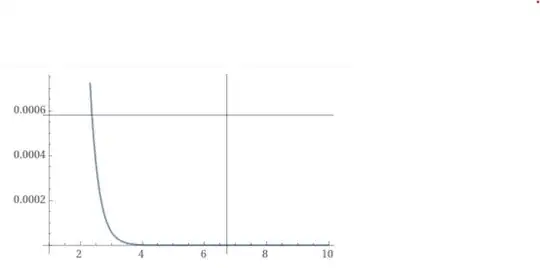But in order to calculate the radial probability density which is actually observable we just need a function of the form: $$p(r) = 4 \pi r^2 |e^{-2r}\ U(\frac{1}{2},2,4r)|^2.$$ This seems well-behaved at $r=0$ and $r\rightarrow\infty$. psmall plarge WolframAlpha says: $$\lim_{r\rightarrow 0^+}4\pi r^2|e^{-2r}\ U(\frac{1}{2},2,4r)|^2=\frac{1}{4}.$$ Therefore is $n=1/2$, $l=0$ a valid hydrogen wavefunction?

John Eastmond
  • 6,111

1 Answers1

8

The wave function must be in the domain of the observables $p,p^2, 1/r$, that is $$\int_0^\infty r^2 dr (U/r)^2 <\infty$$ and $$\int_0^\infty r^2 dr (U''(r))^2 <\infty $$

but we have

$$\underset{r\to 0}{\text{lim}}e^{-r} r^2 \left(\frac{\partial }{\partial r}U\left(\frac{1}{2},2,r\right)\right)^2 = \infty$$

and $$\underset{r\to 0}{\text{lim}}e^{-r} r^2 \left(\frac{U\left(\frac{1}{2},2,r\right)}{r}\right)^2=\infty$$

Both terms diverge at r=0 and thus are not integrable.

$$\text{Series}\left[e^{-r} r^2 \left( \partial_{rr } U\left(\frac{1}{2},2,r\right)\right)^2,\{r,0,1\}\right]=\frac{4}{\pi r^4}-\frac{2}{\pi r^3}-\frac{1}{4 \pi r^2}+\frac{-\log (r)-\gamma +1+2 \log (2)}{4 \pi r}+\frac{4 \log (r)+4 \gamma +1-8 \log (2)}{128 \pi }+\frac{r (4 \log (r)+4 \gamma -1-8 \log (2))}{256 \pi }+O\left(r^2\right)$$

The fact that a function solves the eigenvalue equation is of no significance. All linear eigenvalue equations over $\mathbb R^n$ of the second order have families of solutions with continuous 2n eigenvalue families. But eigenfunctions as elements in Hilbert space are selected by the choice of eigenvalues yielding square integrable images under $\Delta$ and the potential $V(x)$.

Roland F
  • 81