2

Rabi oscillation of a two-level system is colloquially discussed in textbooks about quantum mechanics (especially quantum optics), so I think I'm good with just stating the results.

The Hamiltonian is given by $$ \hat{H}=\frac{\hbar\omega_0}{2}\hat{\sigma_z}+\hbar\Omega_1\hat{\sigma}_x\cos\omega t $$

At resonance, the usual analysis with the rotating-wave approximation (RWA) yields $$ a(t) = \cos \left(\frac{\Omega_1}{2}t\right) $$ $$ b(t) = -i\sin\left(\frac{\Omega_1}{2}t\right) $$ where $\psi=\begin{pmatrix}a\\b\end{pmatrix}$ with $\psi(0)=\begin{pmatrix}1\\0\end{pmatrix}$.

Using the Bloch sphere representation, $\psi$ rotates about the $x$-axis at a frequency of $\Omega_1$. In other words, it is always in the $yz$-plane.

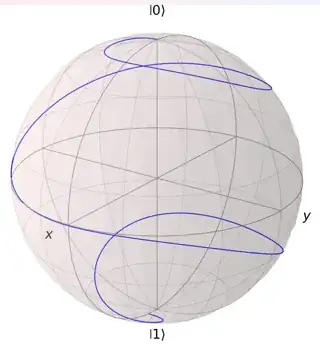
My problem is this: isn't the motion supposed to be a spiraling motion? Numerical simulation shows that indeed the motion traces out a spiral:

Created using QuTiP

Furthermore, the Rabi oscillation should be a precession about the $z$-axis combines with another precession about the $x$-axis, judging from the Hamiltonian. Even when RWA is directly applied to the Hamiltonian,

$$ \hat{H}_{RWA} = \frac{\hbar\omega_0}{2}\hat{\sigma}_z+\frac{\hbar\Omega_1}{2}\left[\hat{\sigma}_x\cos\omega t+\hat{\sigma}_y\sin\omega t\right] $$ I found that the resulting motion still traces out a spiral.

My suspicion is that somewhere in the analytical solution, one moves into the frame precessing along about the $z$-axis. However, I have no way to prove this nor did I see this anywhere in the derivation. But if this were true then the analytical result above would make sense since it is indeed what one would see in the rotating frame, i.e. the vector simply rotates about the $x$-axis. In any case, I am confused with the analytical result.

Tobias Fünke
  • 8,777
hendlim
  • 856

1 Answers1

2

You are right about the frame. To see this, you can go into how one gets the rotation wave approximation. For Schrodinger equation $H\psi = i\partial_t \psi$ we let $\psi=U(t)\tilde\psi$, by which the equation changes into $\tilde H\tilde\psi=i\partial_t\tilde\psi$ where $\tilde H=U^\dagger(t)HU(t)-iU^\dagger(t)\partial_tU(t)$. Here one choose $U(t)= \mathrm{diag}(e^{-i\omega t/2},e^{i\omega t/2})$ and then $\tilde H=\frac{\hbar(\omega_0-\omega)}{2}\sigma_z+\frac{\hbar \Omega_1}{2}\left[\sigma_x+\left(\begin{array}{cc}0&e^{i2\omega t}\\e^{-2i\omega t}&0\end{array}\right)\right]$. With resonance $\omega_0-\omega\sim 0$ we drop the first term, while in RWA we also require $\omega \gg \Omega_1$ so that the $2\omega$ term leads to fast oscillation, which is unimportant in the long time scale. Then the Hamiltonian is just $\frac{\hbar \Omega_1}{2}\sigma_x$ and for $\tilde\psi(0)=\psi(0)=(1,0)^T$ we have $\tilde\psi(t)=(\cos\frac{\Omega_1}{2} t,\sin\frac{\Omega_1}{2} t)$, which seems rotating in xz plane but in fact $U(t)$ represent rotation along z direction with frequency $\omega/2$, the actual wave function $\psi(t)$ will be a spiral motion as you thought.

Black Monolith
  • 596