Vacuum polarization

Question

Interaction vertex of QED are like: \begin{equation} e \bar{\psi} {A\mkern-9mu/} \psi \end{equation}

But we can't write a vertex where a particle-antiparticle pair annihilates in just 1 photon, due to conservation of energy in the centre of mass.

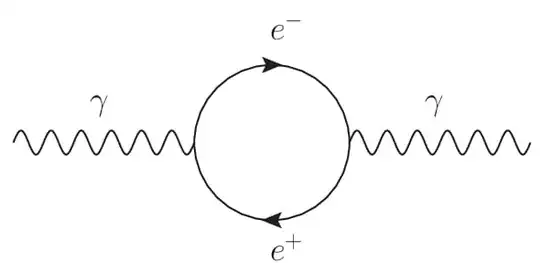
How can we write the vaccum polarizations as:

Where the arrows are for Dirac indices.

I recall something like "you need to make it interact with a heavy nucleus" and it makes sense, but where do I put it in the diagram? A 4 legged vertex means that's no more QED.

Answer 1

Virtual particles are off-shell, so they are not constrained by relations such as $p_\mu p^\mu=m^2$. This diagram is perfectly fine without any external field; no need for heavy nuclei.

Answer 2

This answer agrees the existing one and expands a little.

The question correctly asserts that each vertex in the diagram would be ruled out by energy/momentum conservation if we were talking about either classical particles or a vertex in a Feynman diagram with all external legs. In the interior part of a Feynman diagram vertices like this are not just allowed but positively have to be included. They conserve energy and momentum but this implies the 'particles' concerned are not particles but virtual particles. They don't propagate in the same way as particles owing to a decaying exponential as compared with a free-propagating term where the exponential has a purely complex argument. If we calculate $E^2 - p^2$ for the virtual particles we will not typically get the square of the rest mass of any known particle. This is what is meant by calling them 'off-shell'.