If the plot is in Schwarzschild coordinates then it appears to be correct. Ity should also be symmetric in the sense that light geodesics are reversible - the light should be able to follow them in either direction. The confusion over the limiting angle at which light can escape is just due to confusion over in which frame of reference the angle is measured.
I think the maths is the following: The equations of motion written in Schwarzschild coordinates are
$$\frac{dr}{dt} = \pm \frac{b}{r_s}\left(1 - \frac{r_s}{r}\right)\left( \frac{r_s^2}{b^2} - \left(1-\frac{r_s}{r}\right)\frac{r_s^2}{r^2}\right)^{1/2}\ , $$
and
$$ r\frac{d\phi}{dt} = \frac{b}{r}\left(1 - \frac{r_s}{r}\right)\ $$
where $r_s$ is the Schwarzschild radius and $b$ is the impact parameter of the light (the ratio of its angular momentum to its energy, as measured far from the black hole).
If we construct a right angled triangle then the angle $\theta$ the trajectory makes with the radial direction is given by
$$\theta = \tan^{-1}\left[\frac{r d\phi/dt}{dr/dt}\right] = \tan^{-1}\left[\frac{r_s}{r}\left( \frac{r_s^2}{b^2} - \left(1-\frac{r_s}{r}\right)\frac{r_s^2}{r^2}\right)^{-1/2}\right]\ . $$
Thus if you have a trajectory with $b$ just larger than $3\sqrt{3}r_s/2$, then at the photon sphere we have $r=1.5r_s$ and $\theta = \pm \pi/2$. Then, when $r=r_s$, $\theta = \tan^{-1}(3\sqrt{3}/2)=68.9^{\circ}$ (and not $\sin^{-1}$?). This appears to match your plot and I see something similar using the GRorbits software (see below; note, the axes are in geometrised units where $r_s=2M$).
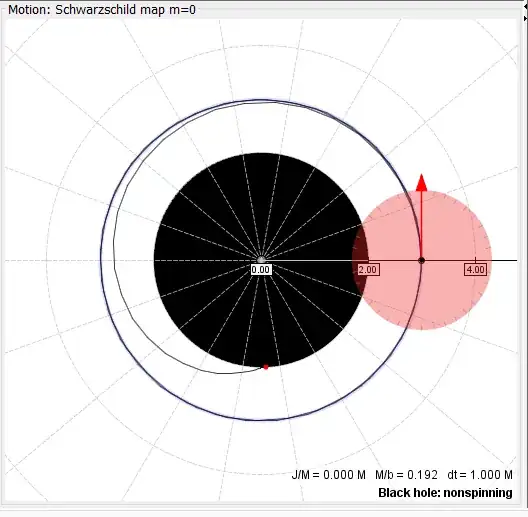
Starting just inside the photon sphere - the time-reversal of this would not escape.
Note that the time reversal of this trajectory (and the one you plotted), won't quite escape the black hole. A time-reversed escaping trajectory would start just above the photon sphere angled slightly inwards. Here is one I produced in GR orbits, but you can see that the angle at which it meets the event horizon is imperceptibly different.
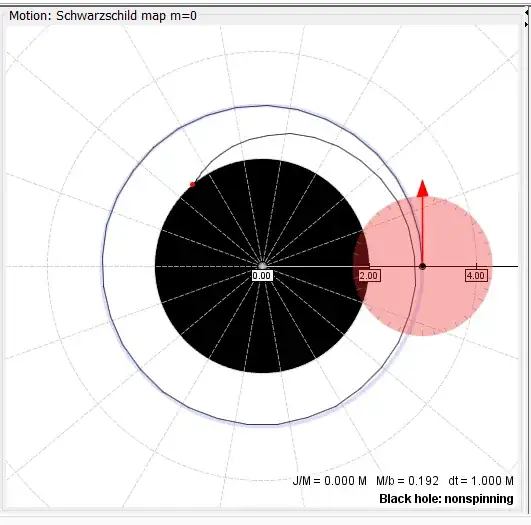
Starting just outside the photon sphere - light would escape if time reversed
The notion that in order to escape, light must be emitted almost radially from just above the event horizon is not correct in Schwarzschild coordinates but it is correct when considered in the coordinate system of the local inertial frame of an observer hovering just above the event horizon. For the full details of that you can see https://physics.stackexchange.com/a/787543/43351
And I hope, to finally make this clear, I show one further plot from GRorbits. This shows the trajectory of light launched from $r=1.001r_s$ that just escapes from the black hole (with $b = 2.5980r_s$). The red arrow shows the direction in which this light is launched in the frame of reference of the observer at $r=1.001r_s$. You can see that this is almost radial (the angle is 4.7 degrees to the radial), but the angle that the light trajectory makes to the event horizon is almost identical to those shown in the pictures above and is distinctly non-radial.
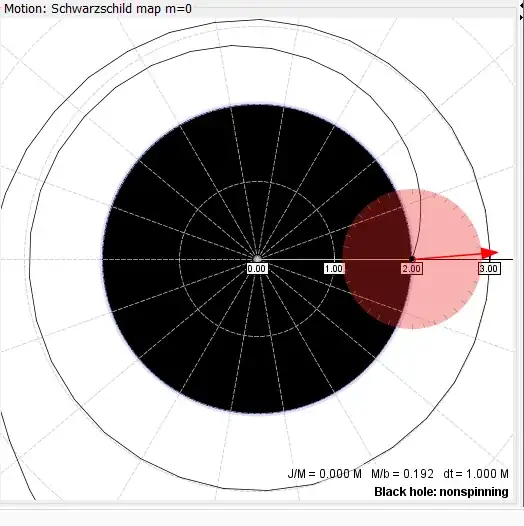
Light launched (almost) radially from $1.001r_s$ that just escapes the black hole. The arrow shows the launch vector (4.7 degrees to the radial) in the local frame of reference of the light source.




