So lets say if there is a hypothetical space craft capable of surviving the gravity of the neutron star and the heat, and say they are on the surface of a neutron star that is about 2.2 times the mass of the sun. How perfect would their escape have to be to actually escape, assuming they are on full thrust. Would any slight disruptions cause them to crash land into the surface? Is this true for light as well?
2 Answers
In Newtonian physics there is just a single "escape speed" for a body with some mass and gravitational field. If you launch an object at greater than this speed and outward fro the surface at any angle, then that object has a total energy (kinetic, potential and rest-mass) $>mc^2$ and will escape to infinity.
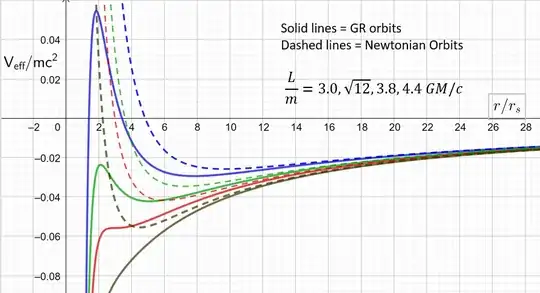
This is not necessarily the case in General Relativity. If we consider the Schwarzschild metric, then the effective potential that a particle moves in can have a local minimum (like in Newtonian physics, which defines the limit of a stable bound orbit) but also, if the specific angular momentum is $>\sqrt{3}r_sc$, a local maximum, which is quite unlike the Newtonian case (see below).
Effective potential in the Newtonian and Schwarzschild (GR) cases as a function of the specific angular momentum ($L/m$). Solid lines show the GR case, dashed lines are the equivalent in Newtonian physics. The solid blue line shows an example where an object launched from a neutron star surface with that value of $L/m$ (i.e. at an angle to radially outward) would need a total energy greater than some threshold corresponding to the local maximum in the effective potential in order to escape to infinity.
The local maximum is at a position $3r_s/2 < r <3r_s$, where $r_s$ is the Schwarzschild radius and if the specific angular momentum of any inertial (ballistic) body is $>2r_s c$ then the local maximum can be such that a body travelling outwards from a radial coordinate less than the local maximum and with total energy of $mc^2$ will encounter a potential barrier and fall back inwards -a so-called trapped orbit.
What this means is that a body launched directly outwards (with no angular momentum) from a neutron star will behave like in Newtonian physics - if its total energy is $>mc^2$ it will escape. However, if the body is launched with the same total energy but at an angle so that it has a specific angular momentum $>2r_s c$ then it is possible for that object to fall back towards the neutron star surface after attaining a maximum radial coordinate somewhere between the neutron star surface and the position of the local maximum in the effective potential. i.e. The escape speed becomes dependent on the launch angle.
Something similar happens for light. If a neutron star has a radius of $<1.76 r_s$, then although radially directed light will always escape, there is a threshold angle to the normal to the surface beyond which an emitted light beam will fall back and hit the neutron star surface. For a neutron star of larger radius, light will always escape in whichever (outward) direction is is launched - see How small would a neutron star be to see the entirety of it? . Also see Falling angle of a photon near the event horizon .
- 141,325
When you try to escape the influence of any gravitational body (not just neutron stars), you can have three results:
- Parabolic trajectory - crashing to the surface
- Elliptical trajectory - an orbit
- Escape trajectory
If they have sufficient thrust to escape, but their engine cuts out for just a moment and then recovers, they can still escape so long as their thrust is restored in time to deliver enough acceleration to their spacecraft that is doesn't crash back down first.
Those are your only options. If you lack the ability to make it into an escape trajectory, then you can either recover into an elliptical trajectory or crash down to the surface
As for light, it always moves at $c\approx3\times10^{8} m/s$. Gravity does, however, influence its direction of travel, and in extreme cases can even cause it to orbit or fail to escape.
- 1,845