Is it possible to find the forces in this problem involving a block/beam/bar glued to the side of a wall?

Question

This is a follow-up to a previous post of mine post. In that post, we concluded that a beam cannot be held in place by an application of normal forces in only one location if that location is off the center of mass. That makes complete sense.

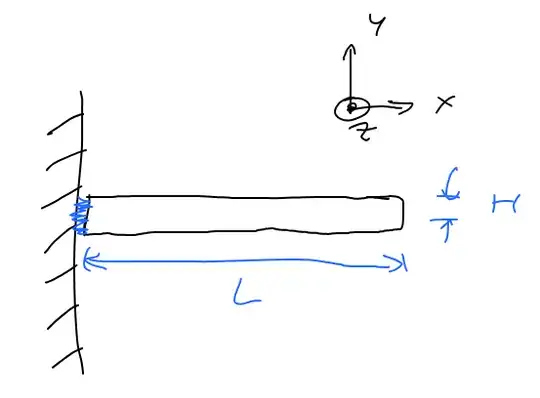
In light of that, I am wondering how we can explain the following modified scenario. Suppose we have a rectangular beam glued to the wall, as depicted below.

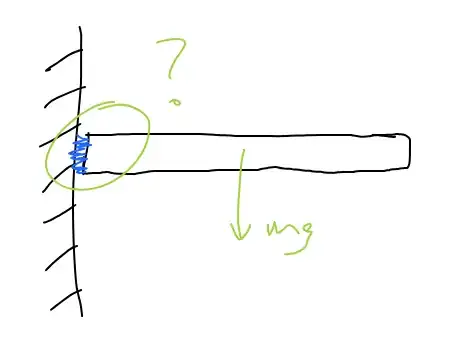
Assume the beam is uniform in density and is of mass $m$. It's length is $L$ and height (really it's the width here) is $H$. The resultant force due to gravity will be $\vec{W} = -mg\hat{y}$ at the center pulling the block downward. The glue has to keep the block from falling, so there ought to be forces on the left side of the block.

Now there can be a combination of horizontal forces and vertical forces applied at the left side.

My first question is, is this an underdetermined problem, meaning more needs to be specified about the contact between the glue and the side of the block? If so, I wonder how that could be dealt with. The example in this post shows that this is a real possibility.

My main question is, since the gravitational force acts downward on the block, there has to be a force upward on the left side by the glue. However, in the post I linked at the start of this post, we can't add only one off-center force acting upward without creating a net nonzero torque. So in terms of forces, how exactly is it possible that the glue can keep the block in place if adding a vertical force upward at the left will lead to a nonzero torque?

Note that my block has a height/width this time, because I think this problem would be unsolvable if it were a 1D rod. However, I'm still unsure how the issue can be resolved.

Answer 1

(This answer assumes that everything but the glue—left support, beam, gravity, etc.—is ideal, as the focus is the glue and the nature of its connection, perfect or imperfect.)

The problem is statically indeterminate as specified, as multiple combinations of valid horizontal force distributions within the glue strip could (1) add up to zero (as required by horizontal equilibrium) and (2) provide a total moment such that the beam doesn't rotate (as required by rotational equilibrium).

Yes, the reason is the same as in the previous post; you have a distributed load that in practice can't be unambiguously determined based on the information given here.

The strategy applied in the typical introductory physics or engineering statics course is to assume the simplest load distribution $w(z)$ (e.g., in N/m) within the glue: tensile at the top of the beam and compressive at the bottom, with the distribution varying smoothly and linearly between those two points—zero at the vertical beam center. The equivalent assumption is that the glue is perfectly applied, uniform, and Hookean, with negligible Poisson effects, etc.

With $w(z)=\frac{w_\text{max}z}{H/2}$, equilibrium then requires

$$\int^{H/2}_{-H/2}w(z)\,dz=0\text{ (horizontal, already satisfied with the Ansazt)};$$

$$\int^{H/2}_{-H/2} zw(z)\,dz-M=0\text{ (rotational)},$$

and $w_\text{max}$ can then be determined from the moment $M$ that must be borne (here, $\frac{mgL}{2}$).

Edit: The question was edited to focus on the vertical force, where the same situation of static indeterminacy arises, as multiple vertical load distributions $y(z)$ could add up to support the downweight load of $mg$:

$$\int^{H/2}_{-H/2} y(z)\,dz-mg=0\text{ (vertical)},$$

The simplest realistic arrangement is to take $y(z)=\frac{mg}{H}$, notwithstanding that real measurements might identify different distributions depending on the glue connection and properties.