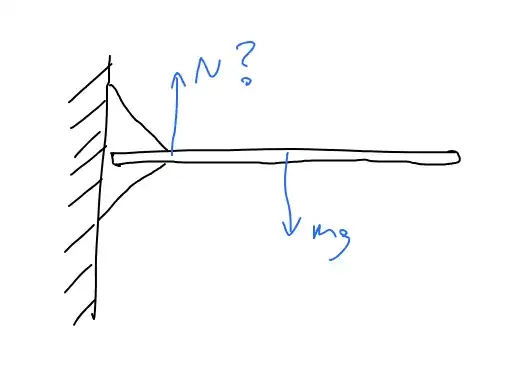
Suppose we have a horizontal rigid bar held in place by two reinforcement beams (one above the bar and one below the bar), both of which are attached to a wall, such that they "clamp" the bar from one side. This system is like a cantilever support, where one end of the bar is held firmly and the other end is free. See the diagram below.
Now let's say the bar is of uniform density and of mass $m$, so there is a gravitational force $mg$ acting at the center. To prevent the bar from falling down, we need some force upward acting on the bar. The only possible other forces are provided by the support beams on the left. Let's say they exert normal forces $N_{1}$ (up) and $N_{2}$ (down).
Now if both support beams touch the bar at exactly the same $x$-coordinate (where we say $x$ is a coordinate of a horizontal axis), the bars supply a force $N = N_{1}-N_{2}$ upward at one $x$-coordinate of the bar.
To prevent the center of mass of the bar from moving, the net force must be zero, so we must have $N - mg = 0$. However, if we consider the torque about the center of mass of the bar, we find the net torque is $\tau = -r_{N}\cdot N + 0\cdot mg \ne 0$. The net torque is nonzero, so the bar must rotate. However, it shouldn't rotate, by design of the problem.
Is there a mistake made in my reasoning leading to this contradiction? Is the assumption that the two support beams touch the bar at exactly the same $x$-coordinate invalid?