Plank overhanging off a building — where does the normal force go?

Question

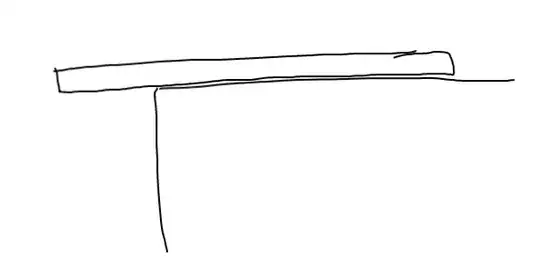
Suppose there is a (uniform rectangular) plank of mass $m$ and total length $L$ that is on top of a building with some piece overhanging or jutting out past the building. Assume it isn't past the point where it tips over, so assume it stays in place. See the image below.

Let's say the overhanging piece is of length $L_{1}$ and the piece on top of the building is $L_{2}$. There are two forces acting on this plank: gravity and the normal force.

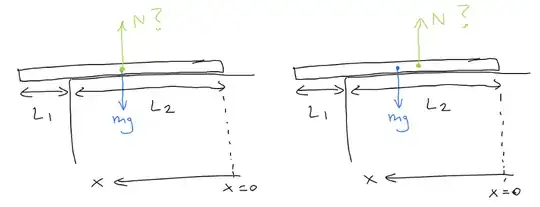
Gravity acts on the entire plank uniformly, so the resultant of the gravitational force will be $F = mg$ downward at the center of the plank, i.e. at $x = L/2$ in the images below.

Now my question is, where does the resultant of the normal force go? Should it be $N$ upwards at $x = L/2$ or at $x = L_{2}/2$? Moreover, what is the magnitude of $N$?

Remember that the plank doesn't tip over, so both the net torque (relative to, say, the pivot at $x = L_{2}$) and the net force have to be zero.

• If the normal force acts at $x = L_{2}/2$, then since the net torque has to be zero, we must have $N < mg$. But if $N < mg$ then the overall net force on the plank body is nonzero, so it must move.
• If the normal force acts at $x = L/2$, then we can set $N = mg$ to get zero net torque and zero net force. However, this doesn't quite make sense to me, because the normal force is only acting on the $L_{2}$ portion of the plank. If it's acting uniformly on the $L_{2}$ piece, shouldn't the resultant act on the middle of that piece? Moreover, if only a fraction of the plank is in contact with the top of the building, shouldn't the overall normal force be less than the usual $mg$?

Which placement and magnitude of the resultant normal force is correct? And why?

Answer 1

Adding to Chemomechanics' answer, the resulting forces is dependent also on the plank's geometry and material. Here's the behaviour of a particular material and geometry of a plank.

Fine, it's actually a piece of paper. But a piece of paper is great because the deformation is highly exaggerated and we can see it with our eyes. A real plank would have similar but less obvious deformations.

As you can see, there's a point force on the ledge and some distributed force at the right end. There's obviously none in the middle because the plank is curved away from the surface.

If the plank is very long, then far enough to the right you'd expect it to behave as if there was no ledge and it would lie completely flat on the surface and have more or less uniformly distributed normal force equal to its weight.

Answer 2

Of the existing answers, one suggests that the reaction force can be represented by two forces, whereas the other says that the force is a distributed force. These aren't incorrect, but they aren't quite consistent.

We can step back and be more general.

In fact the problem is statically indeterminate; various configurations of reaction forces would provide equilibrium, including one force (under the center), two (under the extents of the supported area), a hundred, or an infinite number (i.e., a distributed load). (In practice, there will be two to many contact points bearing the weight, depending on the actual roughness/curvature of the two surfaces.)

Answer 3

It is really a distribution of small force pieces across the entire plank-roof surface.

But it can be simplified as two forces, one at the edge of the building, and the other at the other end of the plank. Then, with two different forces, you can model the full range of behaviour, even up to the point of tipping. You got it correct, the sum of the forces must equal weight for no motion.

Answer 4

For vertical equilibrium the normal reaction force must equal the weight of the plank. But that force is distributed over the length $L_2$ varying linearly from the ledge of the building to the other end of the plank being a maximum at the ledge and a minimum at the other end of the plank. The location of the normal reaction force is that which results in the sum of the moments about any point, the ledge of the building, being zero.

As $L_1$ increases the location of the normal reaction force moves towards the ledge. When $L_1 = L_2 = \tfrac 1 2 L$, where tipping is imminent, the location of all the normal reaction force will be at the ledge in order for the sum of the moments to be zero.

Hope this helps.

Answer 5

As other answers have said, the normal force is distributed along the length of the plank, and it is greater near the edge of the building than at the fan end of the plank. Without making additional assumptions it is not possible to work out the force at every point where the plank rests on the building, and it doesn't matter anyway unless you are an ant stuck under the plank.

There are two obvious ways to analyse the situation. Both are "correct"; which one you use depends on what you are actually trying to find.

1. You can use a single point - you pretend the plank is supported at its centre of mass. This is simple and it works well if you know the centre of mass is above the roof.
2. You can use two points - you pretend the plank is supported at the edge of the roof and at the end of the plank which is over the roof. This lets you get an expression for the normal force at the end of the plank, and varying L2 in this expression will give different values for this force. When this force becomes zero the plank is about to tip.

In general you need to choose the way you analyse a problem according to what the problem is. Choosing the right way can make your work easier and it can make predictions and problems easier to see.

Answer 6

Also adding to Chemomechanics' answer, being indeterminate allows for multiple solutions to support the plank, but if the beam is rigid and static, it has a unique solution if a single force were to be applied, exactly through the center of mass, we can also interpret this as the averaging of the force along the contact surface (this force along the contact surface can be referred to as a force distribution) is equivalent to a force exerted at a point.*

You can use this idea to answer another relevant question like, how far could I, in principle, move the plank over the edge?

the force can't come from beyond the edge of the table, so that means once the center of mass passes the edge, then there's no way for the table to push (not pull) and average out to something that doesn't contact a point where the table touches the plank, so as a result of the force no longer averaging out to push through the center of mass, the plank starts to rotate.

A thought exercise if you'd like it: suppose someone comes up to push a box (something that has width and height), the floor produces some amount of friction and the box has contact with the floor, how might you figure out if the box will slide without starting to rotate?

a tip to this exercise:

note that we're interested in the same condition as before, what needs to happen to cause a body to rotate? But now there's a force from the person pushing as well as friction and normal force from the floor.

* we can extend this to other moments of the force distribution. The idea of torque is about how an action from a force not through the center of mass can rotate a rigid body, so we can also condense the force distribution to exert a torque at a point in addition to the average force at a point, this extends to higher moments as well, but these don't get names in mechanics. These notions are exactly those from statistics and probability as the "distribution of a force" is very similar notion of "distribution" in the term "probability distribution".

Answer 7

Treat the plank as two parts. Part A, resting on the ground. And part B hanging. The condition for balance will be that part A with its mass (its mass should be calculated proportional to the length) is causing a torque in a given direction. The hanging part, with its hanging mass, is giving a counter torque. The pivot is the point when it the resting mass ends, and after which the hanging mass starts.

mgl for the hanging part = mgl for the resting part.