How strong of a gravitational field do you need for a projectile to make a full loop? By full loop I mean it curves once around the by dot, and then it ends up on the same trajectory as it was one before it approached. How many times the Schwarzwald radius would the projectile have to get for this to be possible?
I know the limit in Newtonian gravity is half a loop.
Here's an extension of my previous answer to include some computations.
We'll parameterize the motion in terms of asymptotic speed $\beta=v/c$ of the particle, and its impact parameter $b_i$. These are related to the energy $E$, the angular momentum $L$, and the two length scales $a,b$ (as defined in the other answer) by
\begin{align} \gamma = \frac{E}{mc^2} &= \frac{1}{\sqrt{1-\beta^2}} \\ L = \left|\vec r\times \gamma m \vec v\right| &= b_i \cdot \gamma m v \\ a = \frac hc = \frac L{mc} \color{lightgray}{{}\cdot\frac{\gamma\beta}{\gamma v/c}} &= \gamma\beta b_i \\ b &= \beta b_i \end{align}
Switching to $u=1/r$, the differential equation describing the motion is \begin{align} \left( \frac{\mathrm du}{\mathrm d\phi} \right)^2 &= b^{-2} - \left( 1-ur_s \right)\left( a^{-2} + u^2 \right) \\&= r_s(u-u_1)(u-u_2)(u-u_3) \end{align}
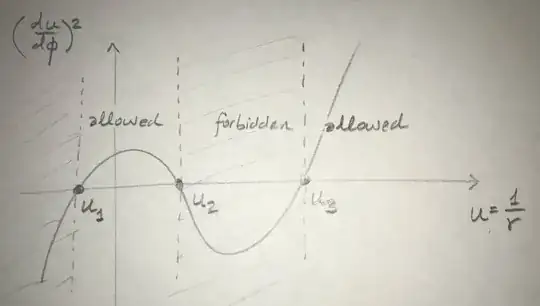
For particular values of $\beta,b_i$, we can plot this equation and find its roots numerically:
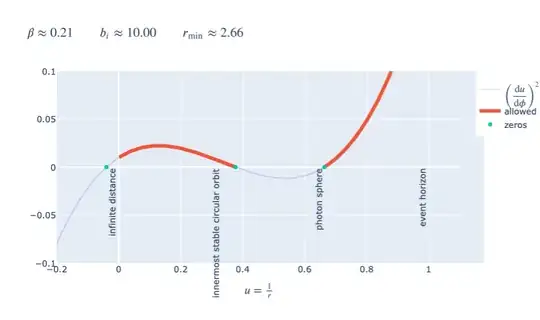
Since the cubic equation describes the square of the derivative, motion is only allowed in regions where the curve is positive (in red). The left red segment describes a particle approaching from infinitely far away $(r^{-1}\to 0)$, turning around at the root $u_2$ somewhere inside of the innermost stable circular orbit at $3r_s$, and escaping to infinity again. The red segment on the right describes a particle with this same total energy but an initial condition too close to the event horizon to escape; that particle can get as high as $u_3$, but then it'll crash into the event horizon.
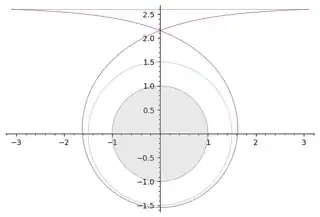
Aiming the particle closer to the black hole brings the turning points $u_2,u_3$ closer together. Here we reduce the impact parameter $b_i$ by about 5%:
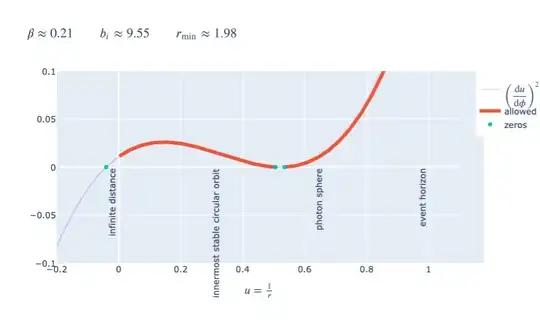
If the impact parameter is too small, the curve for $(\mathrm du/\mathrm d\phi)^2$ becomes positive on the entire interval $(u_1,\infty)$. That describes a particle which eventually reaches the event horizon, and thence the singularity. Note that the sign of the always-real root $u_1$ determines whether the orbit is unbound escaping to infinity, or bound.
This critical impact parameter $b_i^\text{critical}$, where the centrifugal barrier is too small to eject the particle and it is captured, exists for every asymptotic speed $\beta$. If we look at plot of the closest approach between the particle and the singularity on the $(\beta, b_i)$ plane,
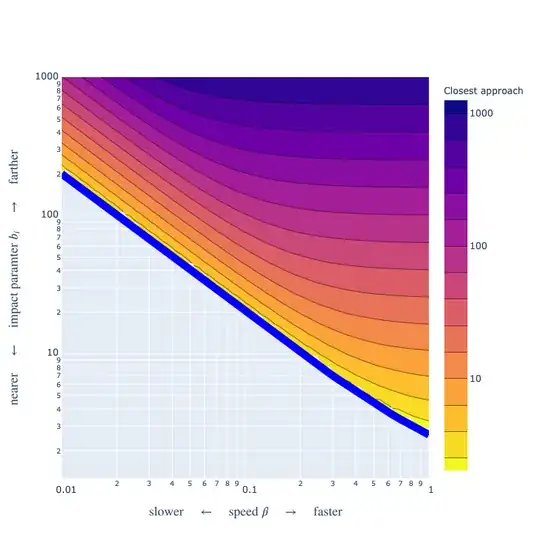
we see that in the "fast, far" corner the closest approach is not substantially different from the impact parameter: these particles have trajectories that are barely affected from the black hole. Particles whose impact parameter is below the blue curve, on the other hand, are captured. Along the boundary line, the closest approach tends toward $2r_s$ in the non-relativistic limit $\beta\to0$, while the closest approach tends toward the photon sphere at $1.5r_s$ in the relativistic limit $\beta\to1$.
The unbound and not-captured orbits, with three real roots, have the exact solution $$ u(\phi) = u_1 + (u_2-u_1)\ \text{sn}^2 \left( \frac12\phi\sqrt{r_s(u_3 - u_1)} + \delta \right), $$ where $\text{sn}$ is a special function. (This may actually hold for more orbits, but my implementation of $\text{sn}$ doesn't seem to accept complex arguments.) This position function is periodic with period $$ 2K(m) = \int_0^{\pi/2} \frac{\mathrm d\theta}{\sqrt{1-m\sin^2\theta}} $$ where the parameter is $$ m = \frac{u_2-u_1}{u_3-u_1} $$ In the limit $u_2\ll u_3$, or $m\to0$, this gives us Newtonian orbits without any precession. In the other limit $u_2\lesssim u_3$, or $m\to 1$, this period becomes arbitrarily long.
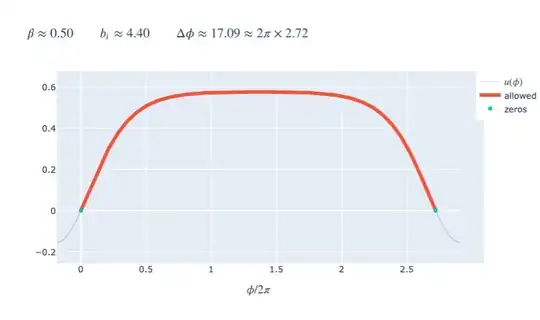
Below is a plot of the equation of motion $u(\phi)$ for the asymptotic speed $\beta = 0.5$ and impact parameter $b_i = b_i^\text{critical} + \delta$, where $b_i^\text{critical}\approx 4.4\,r_s$ and $\delta = 12\times10^{-6}r_s$. The particle comes in from infinity $(u=0)$, hangs out for a while in the region $1.5\,r_s<r<2\,r_s$, then goes symmetrically off to infinity again. If the trajectory were undeflected, the difference between the initial and final $\phi$ would be $\Delta\phi \approx 2\pi\times\frac 12$. But here we have $\Delta\phi\approx 2\pi\times\left(\frac12 + 2.25\right)$: the particle's trajectory winds around the black hole twice, plus a bit, as you've asked about in your question.
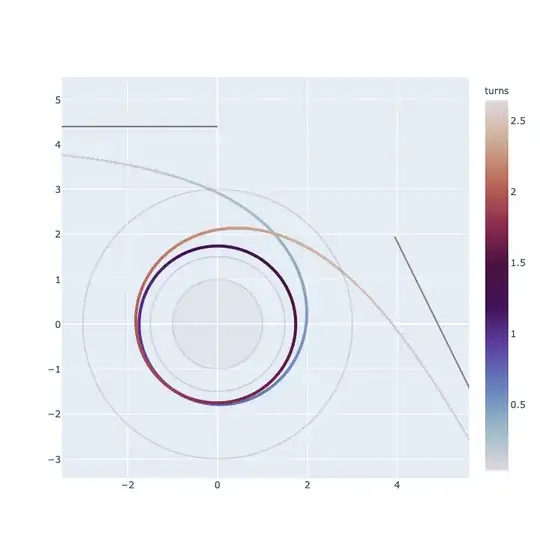
Above is a plot of the trajectory in space corresponding to these same parameters. The black hole is centered at (0,0), and surrounded by
The two straight lines show the asymptotic trajectories with impact parameters $b_i\approx 4.4\,r_s$, while the colored curve shows the path of the particle as it approaches, winds around the black hole twice, and scatters away about a quarter-turn further.
Let's define the "winding number" as $W = \Delta\phi - 2\pi\times\frac12$, so that a straight trajectory has winding number zero, and a one-loop trajectory has winding number one, and so on. When we plotted closest approaches in the $(\beta,b_i)$ plane, we had a lot of empty space on the figure, so we'll plot in the $(\beta,\delta)$ plane instead:
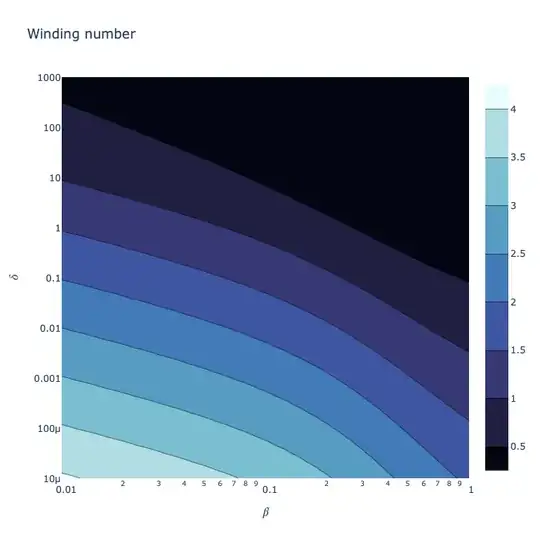
You can see that it's a lot easier to get multiple loops if your particle is nonrelativistic at infinity, $\beta\to0$. However, getting multiple loops requires your particle to come very close to being captured in any case. This suggests that essentially all of the orbits with large winding numbers $W>1$ are going to spend all of their interesting time loitering around their closest approach, with $1.5\,r_s < r \lesssim 2\,r_s$.
In a comment, you seem to be asking a slightly different question: how far can the closest approach be, while still getting a winding number of one (or more)? We can answer that by setting the least-positive root $u_1$ of the differential equation to zero, which is the boundary between bound and unbound orbits. (In the Newtonian limit, $u_1=0$ gives a parabolic trajectory.) Because the roots of the cubic obey the constraint $$ u_1 + u_2 + u_3 = \frac1{r_s}, $$ the equation of motion becomes $$ u_\text{escape}(\phi) \to u_2 \ \text{sn}^2 \left( \frac\phi2 \sqrt{1-r_s u_2} +\delta \right), $$ whose period is now exactly $$ \Delta\phi = \frac{2K(m)}{\sqrt{1-r_s u_2}} ,\qquad \text{with } m \to \frac{u_2}{u_3} \to \frac{u_2}{r_s^{-1}-u_2} . $$
The divergence around $u_2 = \frac{1}{2r_s}$ is very sharp. Poking around on a graph a bit gives
| winding number $W$ | $\frac12-u_2$ | $r_2$ |
|---|---|---|
| 0 (forward scattering) | $u_2\to0$ | $r_2\to\infty$ |
| 0.5 | $0.047\ 3$ | $2.209$ |
| 1.0 | $0.005\ 10$ | $2.020\ 6$ |
| 1.5 | $0.000\ 553$ | $2.002\ 21$ |
| 2.0 | $0.000\ 060\ 0$ | $2.000\ 240$ |
Note that the "impact parameter" is not well-defined if the momentum doesn't stay positive at infinite distance. But this is the furthest you can stay away from the black hole and forward-scatter with nonzero winding number: about 1% further than the critical distance for being captured.
The trajectory you're asking about isn't allowed in Newtonian gravity, where all orbits are conic sections. I'll refer to the gravitator as a "black hole" just to emphasize that general relativity is required.
If the massive particle approaches in the hyperrelativistic limit $\gamma=(1-v^2/c^2)^{-1/2}\to \infty$, the results will be the same as for photons. In that case you can probably use the calculator linked at this related answer to find these trajectories numerically.
In the limit where the massive particle is nonrelativistic during its entire travel, we have the Newtonian result, and such a path is forbidden. Note that the speed at closest approach doesn't necessarily have to be very relativistic for the orbit to depart from a conic section, as famously shown by Einstein when analyzing the orbit of Mercury about the Sun.
This means we have a two-dimensional parameter space in the relativistic factor $\gamma$ and the impact parameter (usually written $b$). We can make this parameter space dimensionless by using $(\gamma,b/R_s)$, with $R_s$ the Schwarzchild radius. These parameters have allowed values between one and infinity, with the limits:
\begin{align} (\gamma,b/R_s) &\to (1,\infty) & \text{slow and far: }&\text{ the Newtonian limit} \\&\to (\infty,1) & \text{fast and near: }&\text{ the photon-sphere/capture limit} \\&\to (\infty,\infty) & \text{fast and far: }&\text{ the photon-lensing limit} \\&\to (1,1) & \text{slow and near: }&\text{ your question} \end{align}
A better pair of parameters for actually analyzing this data would be $(1-\gamma^{-1},1-R_s/b)$, which puts your "slow and near" region of interest in the $(0,0)$ corner where you can expand indefinitely using a logarithmic scale. The plot you want to make is a contour plot, in this plane, of the deflection angle of the projectile. The "half loop" will correspond to the 180º contour; the full loop will correspond to the 360º contour. Your question (v1) seems to assume the result will be independent of $\gamma$, but that isn't obvious to me.
A partial answer for now (v2), because I don't actually know yet how to do this calculation. When I'm ignorant I like to start numerically, but the tool linked above doesn't extend to massive trajectories.
Following the Wikipedia article on Schwarzchild geodesics, we can characterize the motion in the following way.
There are two constants of motion: the total energy $E$ and the angular momentum $L$. We normalize these by the mass of the particle:
$$\begin{align} \frac{E}{mc^2} &= \left( 1-\frac{r_s}{r} \right)\frac{\mathrm dt}{\mathrm d\tau} \\ h = \frac{L}{m} &= r^2 \frac{\mathrm d\phi}{\mathrm d\tau} \end{align}$$
The total energy $E$ includes a potential term, so we can have $E<mc^2$ for bound orbits. For unbound orbits, in the asymptotically flat spacetime with $r\gg r_s$, the energy relation is $\frac{\mathrm dt}{\mathrm d\tau} \approx \frac{E}{mc^2} \approx \gamma$, the familiar Lorentz factor from special relativity. Note that in the ultrarelativistic limit $E\gg m$, describing e.g. massless photons, the ratio $hm/E$ may be zero or nonzero.
Like so many orbital problems, the differential equations are easier in the variable $u = 1/r$. If we define the two lengths $$ a = \frac hc \qquad b = a \cdot \frac{mc^2}{E} $$ then the equation of motion becomes $$ \begin{align} \left( \frac{\mathrm du}{\mathrm d\phi} \right)^2 &= b^{-2} - \left( 1-ur_s \right)\left( a^{-2} + u^2 \right) \\&= r_s(u-u_1)(u-u_2)(u-u_3) \end{align} $$
The second step feels like kind of a cheat: we can do it because every cubic polynomial has three complex roots. The general form of such a cubic, for the case where all three roots are real, is sketched below:
Since the square of $\mathrm du/\mathrm d\phi$ must be positive, trajectories are allowed
The three roots are subject to the constraint $u_1 + u_2 + u_3 = r_s^{-1}$, and at most one root, $u_1$, can be real and negative. The case with $u_1 \leq 0$, as in the sketch, corresponds to an outer turning point beyond infinite $r$: an unbound particle.
If we imagine shifting the curve down so that $u_1 = u_2$, the "allowed" region becomes a stable circular orbit; if we imagine shifting the curve up so that $u_2 = u_3$, then the forbidden region (the "centrifugal barrier") disappears and the distant particle can reach the singularity. If I am understanding correctly, the unstable circular orbit always has radius $r_\text{inner} = u_2^{-1} = u_3^{-1}$ in the interval $\frac32 r_s \leq r_\text{inner} \leq 3r_s$, with the minimum value for relativistic particles like photons.
This suggests a qualitative answer to your question. If we compare with the looping photon paths from the related answer linked above,
(source),
we see that the one-loop photon trajectory has turning point $(u_2r_s)^{-1} = r_2/r_s \approx \frac32 + 0.0033$. The distance $\delta \approx 0.0033$ to the photon sphere in those calculations decreases by a factor of $e^{-2\pi}$ for each additional loop. For a massive particle on an unbound trajectory, we can expect the same sort of approaches: you'll start to get loops only for trajectories which are just barely deflected by the centrifugal barrier.
If I were patient and talented like the author of the linked answer, I might integrate the actual equation of motion, $$ u = u_1 + (u_2-u_1)\ \text{sn}^2 \left( \frac12\phi\sqrt{r_s(u_3 - u_1)} + \delta \right), $$ where $\text{sn}$ is a special function.