Considering the probabilistic relationship between the momentum and position of an electron, are the pictures that show the interaction between electrons and positrons an accurate description of particle motion? We often see visuals that represent the probabilistic nature of particles as probability clouds. How can this converge to well-defined paths? (I never studied this subject, this is just knowledge from general physics books and videos.)
3 Answers
One has to be grounded that all mathematical theories, both classical and quantum, are used to model the existing experimental data and predict new data.
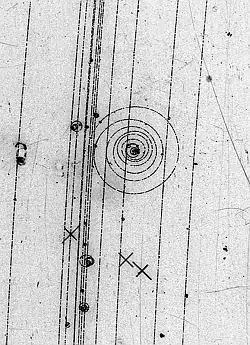
Bubble chamber photograph of an electron knocked out of a hydrogen atom
The curly line was produced by an electron that was struck by one $K^-$ of twelve passing beam particles in a liquid hydrogen bubble chamber. It curves in an applied magnetic field and loses energy rapidly, spiraling inwards.
(To see more particle tracks hit on the "would you like to see" of the link.)
The curving electron track can be perfectly described mathematically by a track made by a classical charged particle curving in the field with the correct energy losses through the medium.
You ask for going from the quantum level to the classical:
How can this converge to well-defined paths?
In this particular picture, the quantum mechanical interaction happens at the vertex , when the $K^-$ interacts with a hydrogen atom with enough energy to knock out an energetic electron. All the bubbles of liquid hydrogen that make up the rest of the tracks comes from very low energy loss , each bubble, from the energy of the track, and although it can be modeled , each bubble , quantum mechanically the next bubble is incoherent, so the trace of bubbles tracks the particle through the liquid with classical equations.
So we call them particles and have confirmed the quantum field theory of the standard model of particle physics, because they leave a macroscopic trace as a classical particle in a magnetic field.
If it walks like a duck and it quacks like a duck it is called a duck.
- 236,935
By the electron-positron interaction I assume you mean feynman diagrams, which do not tell you the exact displacement/position of the particle so it's not breaking the Heisenberg's Uncertainity Principle. Moreover the those diagrams are considering particle interactions rather than wave interactions. You can find a more elaborate explaination of why Feynman Diagrams are drawn with lines even though particles are thought to be field interaction here
Quantum theory describes systems in terms of observables $\hat{X}$ and states $\rho$. The expectation value $\langle\hat{X}\rangle$ of an observable $\hat{X}$ with possible values $x_1,x_2\dots$ is $\sum_j p_jx_j$ where $p_j$ is the probability of the $j$th outcome. This much is uncontroversial.
There are various explanations of what is happening in reality to produce the results of quantum mechanical experiments and some theories that deny any explanation is needed. These explanations are called interpretations for reasons of history and bad philosophy. Interpretations that deny the need for an explanation include the Copenhagen and statistical interpretations. Since they deny the need for an explanation they have nothing to say about we would see a well-defined path for a particle and I won't discuss them further. Other interpretations modify quantum theory. The pilot wave theory postulates particles that exist in addition to reality described by quantum mechanics. Spontaneous collapse theories postulate that the equations of quantum theory should be modified so that every so often a particle's state changes so that it is approximately in a particular place. The implications of those modifications are a subject of ongoing research and it isn't clear why any modifications of quantum theory are necessary so I won't say anything more about them.
In unmodified quantum theory, systems evolve according to particular equations of motion and to work out what's happening you think about what those equations imply. In general if you have a quantum system with more than one possible value to predict the outcome of an experiment you have to look at how all the possible values evolve because they can interfere with one another. And it is possible to do experiments such as single particle interference experiments whose results can only be explained in this way, see "The Fabric of Reality" by David Deutsch Chapter 2 for a popular science discussion of such experiments. Since explaining the results of experiments in general requires taking into account all of the possible states of a system, in general a quantum system doesn't have a single well-defined trajectory. However, if information about the interfering observable spreads to the outside world to a significant extent this prevents interference among the values of that observable: an effect called decoherence. Observables of different systems that have decohered them have strong correlations between them that persist over time. For example, if you measure a charged particle's interaction with water atoms in vapour, then when the particle interacts with one atom it won't be able to interfere with its other versions in different places and the next interaction will be nearby and gradually a trail will form that looks like a trajectory. If you make records of that track in a photo, then the observables of the photo that show the track will be highly correlated with those that instantiate memories in your brain and other records of the photo and those records will persist over time. In general, there will be multiple versions of those records that don't interfere to a good approximation and act a bit like parallel universes: this is often called the many worlds interpretation, but it's just a consequence of quantum theory:
- 11,359
- 1
- 16
- 33