I want to visualise an test EM field in Kerr spacetime (I want to plot the integral field lines). The field is a test field in the sense, that it doesn't change the background (metric).
Could anyone point me to some more technical literature or some Mathematica/python code that would help me?
What I thought I would do: I have the field $F^{\alpha \beta}$ in Boyer-Lindquist coordinates. I then took the ZAMO tetrad (observer family) $e^\alpha_a$ with $e^\mu_0 = u^\mu$ is the for velocity normalized to $$u_\alpha u^\alpha = -1.$$ I then projected the EM tensor onto the tetrad $$ F^{\alpha \beta} e_\alpha^a e_\beta^a = F^{ab} $$ and from this I took the standard definition of electric field $$ E^\alpha = -\frac{1}{2} F^{\alpha \beta }u_\beta \implies E^a = -\frac{1}{2} F^{a0} $$ So now I have the electric field with respects to the ZAMO tetrad.
But how do i visualize this? The tetrad is still expressed in Boyer-Lindquist coordinates (which are like spheriodial coordinates). Do I have to transform into Kerr-Schild coordinates which reduce to cartesian (minkowski) in the flat-spacetime limit?
I hope it's obvious from the context, but I used Greek letters $\alpha \beta$ to denote the indices with respect to coordinates and Latin letters $ab$ to denote indices with respect to tetrad.
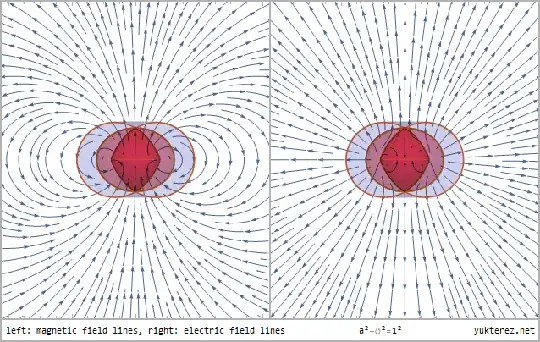
For example I would like to plot something like figure 2 and figure 3 in this article.
Edit: The question can also be reduced to - do I always need to transform to cartesian like coordinates when plotting fields on curved background.