6

The only question I found is this one, but this considers as non-rotating neutron star collapsing:

Our final and most comprehensive test is represented by the collapse to a BH of a magnetized nonrotating star.

When a neutral star with a magnetic field collapses to form a black hole, what happens to the magnetic field?

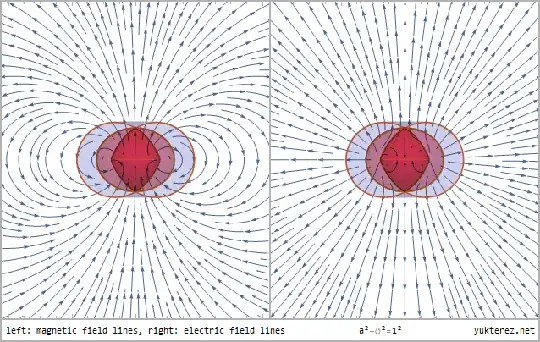
Whenever a rotating (maybe magnetar) collapses into a black hole, the collapse causes a few things I would mention:

  1. the gravitational field remains and is still extending outside the event horizon (though its structure and effects might change at certain distances)

  2. the rotation (angular momentum) remains

  3. the magnetic field disappears

Now this new astrophysical (and never fully formed in our external view) black hole loses its magnetic field though it keeps its angular momentum, and I see some contradiction here, because the magnetic field of the magnetar (or other neutron star) has at least something to do with its angular momentum. Now on top of this, this astrophysical black hole is never even fully formed (from our external view), then how does it lose its magnetic field while it is still rotating?

Question:

  1. How come the magnetic field disappears when a neutron star becomes a black hole, while the rotation remains?
Árpád Szendrei
  • 30,008

1 Answers1

1

Árpád Szendrei asked: "How come the magnetic field disappears when a neutron star becomes a black hole?"

If a net electric charge remains, the star would collapse to a Kerr Newman black hole which does have a magnetic field:

magnetic and electric field lines

What happens if the net electric charge of the collapsing magnet was zero is a different story though, since I don't have a metric for this yet maybe someone else can answer that.

In my opinion it should radiate away its magnetic properties then as it would in the nonrotating case, since the same arguments as in the nonrotating case should still apply here, but I'm not ready to bet on that.

The Kerr Newman family allows only for an electric net charge that generates the magnetic field lines since rotating charges produce magnetism, and you can extend that to a dyonic black hole including some unphysical magnetic monopole, but there is no metric for an electrically neutral black hole with a magnetic dipole and as far as I know no attempts to find one, so I strongly suspect that is ruled out by the no hair theorem.

The only way I could think of to confirm this would be a numerical simulation where you feed in the initial conditions and see how the metric evolves, but for that you'd need a supercomputer. If that was already done they must have found no remaining magnetism, otherwise they would have published it as a refutal to the no hair theorem.

Yukterez
  • 14,655