If a Kerr-Newman black hole is like a charged, spinning, heavy magnet, what kind of magnet is it like?

Question

I was reading up on De Sitter spaces, which states that the gravitational effects from a black hole is indistinguishable from any other spherically symmetric mass distribution. This makes a lot of sense to me.

I'm now super curious, can we just formulate all the properties of a black hole beyond the limit at which GR is needed in a completely Maxwellian / Newtonian sense? The Wikipedia article on the Kerr-Newman metric seems to indicate so, but the equations are in terms of the GR metrics. This is not what I want, I want a simplification, a limit-case of that math.

Ted Bunn answered a part of my question in Detection of the Electric Charge of a Black Hole. Let me repeat the stupidly simple form of the gravitational and electric field for a black hole beyond the point at which GR is needed.

$$\vec{g} = \frac{GM}{r^2} \hat{r}$$

$$\vec{E} = \frac{Q}{4\pi\epsilon_0 r^2} \hat{r}$$

Correct me if I'm wrong, but these would be a meaningful and accurate approximation in many, in fact, most situations where we would plausibly interact with a black hole (if we were close enough that these are no longer representative, we'd be risking a date with eternity).

Question: Fill in the blank; what would the magnetic field $\vec{B}$ around a black hole be?

Here is why I find it non-trivial: Every magnet in "our" world has some significant waist to it. So here is a normal magnet.

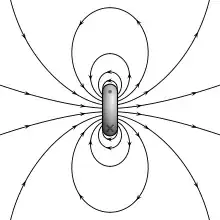
What happens when this is a black hole? Would the approximation for $\vec{B}$ that I'm asking for have all the magnetic field lines pass through the singularity? Or would they all pass through the event horizon radius but not necessarily a single point?

---

I think most people who have understood this already, but ideally the answer would use the 3 fundamental metrics of a black hole. Mass $M$, charge $Q$, and angular momentum $L$. The prior equations for gravity and electric field already fit this criteria. So the answer I'm looking for should be doable in the following form.

$$\vec{B} = f \left( M, Q, L, \vec{r} \right) $$

Answer 1

It's a little tricky giving a formal answer to this, but here is a sketch:. The electromagnetic potential of the Kerr-Newman hole is given by:

$$A_{a}dx^{a}=-\frac{Qr}{r^{2}+a^{2}\cos^{2}\theta}\left(dt-a \sin^{2}\theta d\phi\right)$$

This field will acquire a magnetic field from the fact that $\frac{\partial A_{\phi}}{\partial r}$ and $\frac{\partial A_{\phi}}{\partial \theta}$ are both nonzero. The problem is that the magnetic field, when re-phrased in terms of vectors and not one-forms, will fall off as $\frac{1}{r^{3}}$. At that point, if we're keeping terms that fall off that quickly, then we need to have a discussion about that asymptotic form of the metric you imply above, because there are terms in the metric that we need to keep, arising from frame-dragging effects of the black hole. If you want, I can go into more detail.

EDIT:

OK, so once we have the vector potential, we can calculate the magnetic field according to the rule: $B^{i}=\frac{1}{\sqrt{\left|g\right|}}\epsilon^{ijk}\left(\frac{\partial A_{j}}{dx^{k}}-\frac{\partial A_{k}}{dx^{j}}\right)$, where $\epsilon^{r\theta\phi}=1$, $\epsilon^{ijk}=-\epsilon^{jik}=-\epsilon^{ikj}$ and $\epsilon^{ijk}=0$ if $i=j$, $i=k$ or $j=k$. So, now, we just plug in the above expression for the spatial components of $A_{a}$, the metric tensor, and turn the crank.

After doing this, and taking the limit that $r$ is larger than everything else, we find that

$${\vec B}=\frac{2Qa\cos\theta}{r^{3}}{\hat e}_{r} + \frac{Qa \sin \theta}{r^{3}}{\hat e}_{\theta}$$

Sensibly, this is zero if either $Q=0$ or $a=0$. And I will once again assert that there are $\frac{1}{r^{3}}$ corrections to the gravitational force that must be taken into account in your high $r$ limit if you are going to keep this magnetic field.

Answer 2

I'm going to answer this question with the a priori assumption that if some amount of matter collapses with a given field, then those fields are maintained as it collapses into a black hole. I see nothing to refute this assumption, but the validity of it is beyond my knowledge. As I was pointing out before, this sufficiently far from the singularity such that GR specific concepts aren't needed. The cutoff for this is formalized by the following condition.

$$GM/r \ll c^2/2$$

Again, we have $Q$, $M$, and $L$ to describe the black hole. Obviously the black hole, and the singularity itself is some amount of mass rotating. I find this problematic due to difficulties with loop singularities in a completely Newtonian sense. Anyway, I need to make statements about the angular momentum.

$$L = M a V$$

This is to say, the angular momentum is due to the fact that the mass of the singularity is located at some position away from the axis of rotation, $a$ and spinning at speed $V$. With the above statement we can make some meaningful statement about the magnetic moment, $\vec{m}$. I'll assume the axis of rotation is the z-axis and denote that unit vector with $\hat{k}$. The following equation comes from Wikipedia. I will then combine this with the prior equation. Doing this algebra makes the assumption that the mass has the same distribution as the charge.

$$\vec{m} = \frac{1}{2} Q a V \hat{k}$$

$$\vec{m} = \frac{Q L}{2 M} \hat{k} $$

This does make intuitive sense to me. The more angular momentum, the stronger I expect the magnetic field from it to be. Also, since angular momentum has mass as a component, we basically have to divide that back out. Next, I would just use the equation for a perfect magnetic dipole. This is to say the waist is zero, basically assuming it's a singularity. I think this would be fine unless the rotational energy was a significant part of the energy contained in it. I'll just ignore the delta function for the infinite magnetic field at the origin, because this isn't valid there anyway.

$$\vec{B}(\vec{m}, \vec{r}) = \frac {\mu_0} {4\pi r^3} \left(3(\vec{m}\cdot\hat{r})\hat{r}-\vec{m}\right)$$

$$\vec{B}(M,Q,L,\vec{r}) = \frac {\mu_0 Q L} {8 \pi r^3 M} \left(3 \frac{r_z}{r} \hat{r}-\hat{k}\right)$$