2

I have been reading about physics engines and I am confused on how one approaches simulating collision responses.

I read about the coefficient of restitution:

https://en.wikipedia.org/wiki/Coefficient_of_restitution

But it wasn't clear how this idea could be extended to 3d with rigid bodies. Conceptually you could make contacts non-hard and integrate a force + damping term over a number of iterations dependent upon penetration depth but that is not how engines with hard contact constraints work which is what I am interested in.

FourierFlux
  • 1,002
  • 8
  • 17

2 Answers2

1

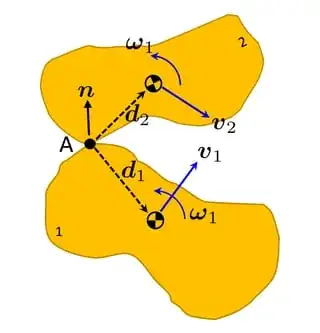
$\newcommand{\b} {\mathbf}$ Assume two particle collied in 3D

the equations are

\begin{align*} &m_1\,(\mathbf v_1-\mathbf u_1)=-\lambda\,\mathbf n\tag 1 \end{align*} \begin{align*} &m_2\,(\mathbf v_2-\mathbf u_2)=\lambda\,\mathbf n\tag 2 \end{align*} \begin{align*} &\left[(\mathbf v_2-\mathbf{v}_1)+\epsilon\,(\mathbf u_2-\mathbf u_1)\right]\cdot\mathbf n=0\tag 3 \end{align*} you have 7 scalar equations for the 7 unknowns; the 6 components of the vectors $~\mathbf v_i~$ and $~\lambda$

Adding equation (1) and (2) you obtain the conservation of the linear momentum and for $~\epsilon=1~$ the conservation of the energy .

where

  • $\b v_1~,\b v_2~$ velocity after the collision
  • $\b u_1~,\b u_2~$ velocity bevor the collision
  • $m_i~$ particle masses
  • $\b n~$ collision direction vector $\quad,\b n\cdot\b n=1$
  • $\epsilon~$ coefficient of restitution $\quad,\epsilon=0~$ perfectly inelastic collision $\quad,\epsilon=1~$ perfectly elastic collision

Theory

starting with Newton equation immediately after the collision

\begin{align*} &m_i\,\frac{d\mathbf v'_i}{dt}= \pm\, F_c\,\mathbf n\quad\Rightarrow\\ &m_i\,\int_{\mathbf u_i}^{\mathbf v_i}\,d\b v'_i=\pm\int F_c\,\mathbf n\,dt=-\lambda\mathbf{n} \end{align*} \begin{align*} &m_i\,(\mathbf v_i-\mathbf u_i)=\pm\lambda\,\mathbf n\quad i=1,2 \end{align*} $~i=1~$ minus , $~i=2~$ plus

where $~ F_c~$ is the constraint force

Conservation of the energy

\begin{align*} &E=\frac{1}{2}\left(m_1\,(\mathbf{v}_1)^2+m_2\,(\mathbf{v}_2)^2- m_1\,(\mathbf{u}_1)^2-m_2\,(\mathbf{u}_2)^2\right)=0\\ &2\,E=\left(m_1\,\left [(\mathbf{v}_1)^2- (\mathbf{u}_1)^2\right] +m_2\,\left[(\mathbf{v}_2)^2- (\mathbf{u}_2)^2\right]\right)=0\\ &2\,E=\left(m_1\,\left [\mathbf{v}_1- \mathbf{u}_1\right]\cdot \left [\mathbf{v}_1+ \mathbf{u}_1\right] +m_2\,\left[\mathbf{v}_2-\mathbf{u}_2\right] \cdot \left[\mathbf{v}_2+\mathbf{u}_2\right]\right)=0\\ &\text{with}\quad \mathbf{v}_1- \mathbf{u}_1=-\frac{\lambda}{m_1}\,\mathbf n \quad, \mathbf{v}_2- \mathbf{u}_2=\frac{\lambda}{m_2}\,\mathbf n\\ &2\,E=\left(m_1\,\left [-\frac{\lambda}{m_1}\,\mathbf n\right]\cdot \left [\mathbf{v}_1+ \mathbf{u}_1\right] +m_2\,\left[\frac{\lambda}{m_2}\,\mathbf n\right] \cdot \left[\mathbf{v}_2+\mathbf{u}_2\right]\right)=0\quad\Rightarrow\\ &2E=\left[(\mathbf v_2-\mathbf{v}_1)+(\mathbf u_2-\mathbf u_1)\right]\cdot\mathbf n=0 \end{align*} and with the coefficient of restitution $~\epsilon~$ \begin{align*} &\left[(\mathbf v_2-\mathbf{v}_1)+\epsilon\,(\mathbf u_2-\mathbf u_1)\right]\cdot\mathbf n=0 \end{align*}

thus for $~\epsilon=1~$ you obtain the conservation of the energy

Example

assume one dimensional

$$\b u_1=[u,0,0]^T~,\b u_2=[0,0,0]^T~,\b n=[1,0,0]^T$$

you obtain

$$\b v_1=\left[{\frac {u \left( m_{{1}}+m_{{2}}\epsilon \right) }{m_{{2}}+m_{{1}}}}~,0~,0]\right]^T$$ $$\b v_2=\left[-{\frac {m_{{1}}u \left( -1+\epsilon \right) }{m_{{2}}+m_{{1}}}}~,0~,0\right]^T$$ $$\lambda=-{\frac {m_{{2}}m_{{1}}u \left( -1+\epsilon \right) }{m_{{2}}+m_{{1}} }} $$ $$2\,E={\frac {m_{{1}}{u}^{2}m_{{2}} \left( -1+{\epsilon }^{2} \right) }{m_{{ 2}}+m_{{1}}}} $$

Eli
  • 13,829
1

In all three scenarios of two particles, a particle and a 3D body and two 3D bodies the calculation of the impulse magnitude $J$ is the same, once the reduced mass $m^\star$ of the contact is found.

$$ \boxed{ J = (1+\epsilon)\, m^\star \; v_{\rm imp}} $$

where $v_{\rm imp}$ is the relative speed of approach of the two bodies at the point of contact, $\epsilon$ is the coefficient of restitution and $m^\star$ is the reduced mass of the system.

For the three cases above, this is how to calculate the reduced mass given the contact normal direction $\boldsymbol{n}$.

  • Two Particles of mass $m_1$ and $m_2$

    $$ m^\star = \dfrac{1}{\frac{1}{m_1} + \frac{1}{m_2}} $$

  • One Body and One Particle with masses $m_1$ and $m_2$ respectively, and mass moment of inertia tensor ${\bf I}_1$ for the body, as well as the position of the center of mass, relative to the contact point, denoted with the vector $\boldsymbol{d}_1$

    $$ m^\star = \dfrac{1}{\frac{1}{m_1} + ( \boldsymbol{n}\times \boldsymbol{d}_1) \cdot {\bf I}_1^{-1} (\boldsymbol{n} \times \boldsymbol{d}_1) + \frac{1}{m_2}} $$

  • Two Bodies with masses $m_1$ and $m_2$ respectively, and mass moment of inertia tensor ${\bf I}_1$ and ${\rm I}_2$, as well as the positions of the center of mass, relative to the contact point, denoted with the vectors $\boldsymbol{d}_1$ and $\boldsymbol{d}_2$

    $$ m^\star = \dfrac{1}{\frac{1}{m_1} + ( \boldsymbol{n}\times \boldsymbol{d}_1) \cdot {\bf I}_1^{-1} (\boldsymbol{n} \times \boldsymbol{d}_1) + \frac{1}{m_2} + ( \boldsymbol{n}\times \boldsymbol{d}_2) \cdot {\bf I}_2^{-1} (\boldsymbol{n} \times \boldsymbol{d}_2)} $$

The above is the same you will find in the Collision Response Wikipedia article, as equation (5).

Note that $\times$ is the vector cross product, and $\cdot$ is the vector dot product.

It is also identical to equation (8-18) in the Physically Based Modeling, Lecture Notes II for rigid body simulations by Andrew Witkin and David Baraff. SIGCOURSE link

fig1

The exact calculation for $v_{\rm imp}$ is

$$ v_{\rm imp} = \boldsymbol{n} \cdot ( \left(\boldsymbol{v}_1 + \boldsymbol{d}_1 \times \boldsymbol{\omega}_1\right) - \left( \boldsymbol{v}_2 + \boldsymbol{d}_2 \times \boldsymbol{\omega}_2 \right) ) $$

The above-calculated impulse $J$ obeys the law of contact

$$ v_{\rm bounce} = -\epsilon \; v_{\rm imp} $$

Here is an example implementation of the above calculation for two bodies in C#

public class Contact
{
    public Vector3 Position { get; set; }
    public Vector3 Normal { get; set; }
    public double Epsilon { get; set; }

public double GetImpulse(RigidBody2 target, RigidBody2 contact, out double impactSpeed)
{
    double m_1 = target.MassProperties.Mass;
    double m_2 = contact.MassProperties.Mass;
    Matrix3 I_1_inv = LinearAlgebra.Inverse(target.MassProperties.MMoi);
    Matrix3 I_2_inv = LinearAlgebra.Inverse(contact.MassProperties.MMoi);
    Vector3 d_1 = target.MassProperties.CG - Position;
    Vector3 d_2 = contact.MassProperties.CG - Position;

    Vector3 h_1 = LinearAlgebra.Cross(Normal, d_1);
    Vector3 h_2 = LinearAlgebra.Cross(Normal, d_2);

    double m_reduced = 1 / (
          1 / m_1 + LinearAlgebra.Dot(h_1, I_1_inv*h_1)
        + 1 / m_2 + LinearAlgebra.Dot(h_2, I_2_inv*h_2));

    impactSpeed = LinearAlgebra.Dot(Normal, 
         (contact.Velocity + LinearAlgebra.Cross(d_1, contact.Omega)) 
       - (target.Velocity) + LinearAlgebra.Cross(d_2, target.Omega));

    return (1 + Epsilon) * m_reduced * impactSpeed;
}



}
John Alexiou
  • 40,139