1

I am writing a simple physics simulation of a real-life problem, and am having trouble coming up with a closed-form solution.

Problem description

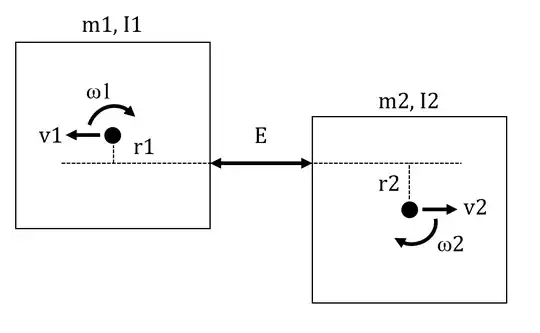
Two rigid bodies with specified masses $m_1$, $m_2$ and moments of inertia $I_1$, $I_2$ are tied together and compress a spring with stored energy $E$. These bodies are initially at rest and lying on a frictionless surface. At a certain time, the line connecting the bodies is cut, and the spring pushes the two bodies apart such that they slide and rotate on the surface. Note that the spring is not permanently attached, so there is no restoring force.

If the spring acts along a line of action with orthogonal distances $r_1$, $r_2$ to each body’s center of mass, then find the resulting velocities $v_1$, $v_2$ and rates of rotation $ω_1$, $ω_2$ for each body.

Here is a top view of this setup:

sketch of scenario

Current approach

This is essentially equivalent to an super-elastic collision problem, with a non-zero energy loss (gain) at the moment of impact. However, I cannot find example of this problem where one of the bodies is not a ball or point mass (which results in one known $ω = 0$, making for three unknowns).

In this case, I have four unknowns: $v_1$, $v_2$, $ω_1$, $ω_2$. I currently have three constraining equations: energy conservation, angular momentum conservation, and linear momentum conservation:

$$E = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2 + \frac{1}{2}I_1ω_1^2 + \frac{1}{2}I_2ω_2^2,$$ $$L = 0 = m_1v_1r_1 + m_2v_2r_2 + I_1ω_1 + I_2ω_2,$$ $$P = 0 = m_1v_1 + m_2v_2.$$

However, I’m lost as to finding a fourth constraining equation. This seems to me like it should have a closed form solution, does it?

Wrzlprmft
  • 6,417
  • 2
  • 28
  • 48
Scott
  • 113

1 Answers1

2

Let's choose our origin to be at a fixed point on the table somewhere along the line of application of the force. The torque on each block about this origin is zero when the spring expands, since $\vec{\tau} = \vec{r} \times \vec{F}$ and $\vec{r}$ is parallel to $\vec{F}$ when $\vec{r}$ is measured about this origin. Thus, the net angular momentum of each block (as measured with respect to this origin) is independently zero: $$ \vec{L}_1 = \vec{L}_2 = 0 \quad \Rightarrow \quad m_1v_1r_1 + I_1ω_1 = m_2v_2r_2 + I_2ω_2 = 0. $$ This is obviously a stronger condition on the angular momentum than you had ($\vec{L}_1 + \vec{L}_2 = 0$), and gives you an extra condition on the parameters that should allow you to solve for the final state.

Alternately, we can derive the same condition by considering the center of mass as our origin for the torque. Let's assume that the force $\vec{F}_1$ is applied at a constant $\vec{r}_1$ relative to the center of mass (i.e., something like a quick, sharp hammer blow.) Then the torque about the CM is $\vec{\tau}_1 = \vec{r}_1 \times \vec{F}_1$, and the total change in angular momentum of block 1 is $$ \Delta \vec{L}_1 = \int \tau_1 \, dt = \int \vec{r}_1 \times \vec{F}_1 \, dt = \vec{r}_1 \times \left[ \int \vec{F}_1 \, dt \right] $$ But the quantity in square brackets here is just the total impulse delivered to the block, and so we have $$ \Delta \vec{L}_1 = \vec{r}_1 \times (\Delta \vec{p}_1) $$ If you carefully keep track of the signs of the vectors and their components, this eventually reduces to $$ - I \omega_1 = m_1 r_1 v_1 $$ as found above; and the same argument applies to block 2 as well.

Michael Seifert
  • 54,357