5 months ago I asked a question about simultaneous collisions Derivation of collision rules. I've been reading about the subject, but, unfortunately, some things are still not clear to me. I implemented a simulator of simultaneous elastic collisions using the method from Baraff's paper Analytical methods for dynamic simulation of non-penetrating rigid bodies https://www.cs.cmu.edu/~baraff/papers/sig89.pdf (section 8. Simultaneous Collisions). He writes:
At every contact point $i$, there is some impulse $J_i = j_i \hat{n}_i$ with $j_i ≥ 0$ the unknown magnitude. The goal is to find a $\vec{j}$ that satisfies the laws of classical mechanics
For contact point $i$, let $v^−_i$ be the relative approach velocity in the $\hat{n}_i$ direction and $v^+_i$ be the (unknown) relative recession velocity in the $\hat{n}_i$ direction. $v^+_i$ is a linear function of $\vec{j}$. If $v^−_i > 0$, the bodies are separating. Otherwise, the bodies are in resting contact $(v^−_i = 0)$ or are colliding $(v^−_i < 0)$
For each contact point in the collision, it is required that $v^+_i ≥ −ε_iv^−_i$
The "≥" is needed since body A might be pushed away from body B by some third body C
the constraints can be written as $v^+_i (\vec{j})+ε_iv^−_i ≥0,\quad j_i ≥0,\quad j_i(v^+_i(\vec{j})+ε_iv^−_i )=0$
To solve this quadratic programming problem, I implemented my own solver, using interior-point method. But what is surprising to me: even though kinetic energy is not explicitly mentioned in the formulation, the simulation manages to conserve it. Of course, the conservation of energy law is "hidden" in the constraint $j_i(v^+_i(\vec{j})+ε_iv^−_i )=0$. But Baraff writes:
The definition of $ε$ does not readily extend to handle simultaneous collisions. The most that can be said is that if each $ε_i = 1$ then no kinetic energy is lost during the collision.
A routine calculation shows that kinetic energy is conserved for multiple collisions when each $ε_i = 1$, and that for single contact point collisions, $v_i^+ = −ε_iv_i^-$
Note that he talks about single contact point collisions. He provides no proof that kinetic energy is conserved for simultaneous collisions of multiple objects and/or with multiple contact points. Just after the quoted text Baraff makes a reference to Classical Mechanics by Goldstein. So I hoped to find something about multiple collisions there, but no luck.
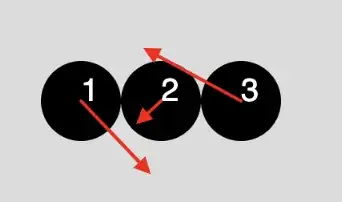
It's easy to show that energy is conserved for this method when the bodies are aligned.
Since tangential components of the velocities stay the same, they can be ignored in the conservation of energy law. So all velocities in the following formulas are velocities along horizontal axis. Also, to simplify, suppose all bodies have the same mass, than: $v_{1f}^2 + v_{2f}^2 + v_{3f}^2 = v_{1i}^2 + v_{2i}^2 + v_{3i}^2$ where $v_{kf}$ - final velocity of the body $k$, $v_{ki}$ - initial velocity of the body $k$
I wrote a MATLAB script that proves that
% impulses
syms j12 j23 positive
% initial velocities
syms v1i v3i v2i positive
% final velocities
v2f = v2i + j12 - j23
v1f = v1i - j12
v3f = v3i + j23
% Newton's impact laws
laws = [v2f - v1f == -(v2i - v1i)
v3f - v2f == -(v3i - v2i)]
% Express j12, j23 as functions of initial velocities
js = solve(laws,[j12,j23])
% Conservation of energy law
K = v1f^2 + v2f^2 + v3f^2 - v1i^2 - v2i^2 - v3i^2 == 0;
% Substitute symbols j12, j23 in the energy law for the functions
proof = subs(K, j12, js.j12);
proof = subs(proof, j23, js.j23)
%returns symtrue => kinetic energy is conserved
simplify(proof)
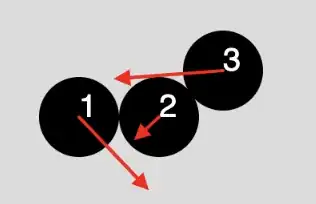
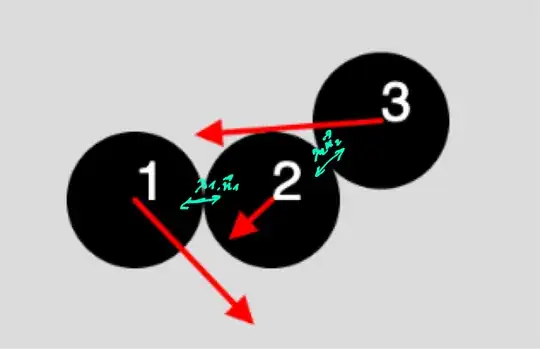
Now, stuff gets more complicated if the bodies are not aligned
I tried splitting velocity of body 2 into normal and tangential components: $v_{2n1f}$ -normal velocity relative to body 1, $v_{2n3f}$ - normal velocity relative to body 3, $v_{2t1f}$ - tangential velocity relative to body 1. Since bodies are not aligned, $v_{2t1f}$ depends on $j_{23}$. Tangential components of velocities for bodies 1 and 3 stay the same and can be ignored, so $v_{1f}$ and $v_{3f}$ - normal components. Formulas I used: $$v_{1f} = v_{1i} - j_{12}$$
$$v_{2n1f} = v_{2n1i} + j_{12} - j_{23}(\vec{n_{23}} \cdot \vec{n_{12}})$$ $$v_{2t1f} = v_{2t1i} - j_{23}(\vec{n_{23}} \cdot \vec{q_{12}})$$ $$v_{2n3f} = v_{2n3i} - j_{23} + j_{12}(\vec{n_{12}} \cdot \vec{n_{23}})$$
$$v_{3f} = v_{3i} + j_{23}$$
$\vec{q_{12}} = \frac{\vec{v_{2t1i}}}{v_{2t1i}}$, so it's a unit vector, perpendicular to $\vec{n_{12}}$
Maybe the formulas are wrong or/and I' missing something. I wasn't able to get the proof that energy is conserved in the same fashion I did for the aligned case using MATLAB.
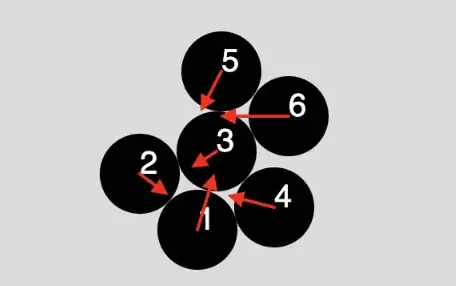
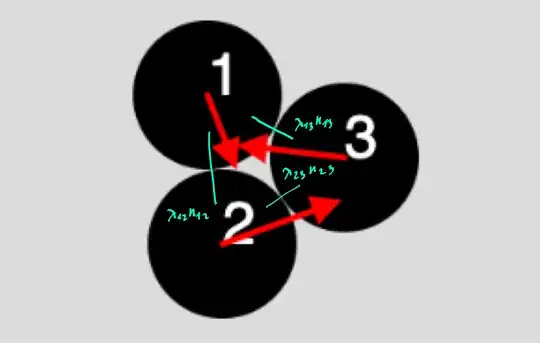
And there are even more complicated cases, where each body has more than one colliding contact point:
I'm aware that the method described in the paper makes many assumptions, which are not realistic. I understand that it's an approximation meant to look plausible for some configurations of bodies. Yet, somehow it does conserve energy.
So, my question is: given that the momentum of the system is conserved and Newton's impact law is satisfied for each colliding contact point, is it possible to prove that kinetic energy of the system is conserved for the arbitrary system of colliding objects? For example:
My question is only about smooth spherical bodies, so no friction and rotation