I have the Lagrangian in 4 dimensions: $$ L = \frac{1}{2}\partial_\mu\phi\partial^\mu\phi-\frac{1}{2}m^2\phi^2+\sum_{i =1,2}\bar\psi_i(i\not\partial-m)\psi_i-g\phi\bar\psi_i\psi_i. $$
Assuming there are $n$ external scalar lines, and no external fermion lines, then the superficial degree of divergence could be found as $\omega = 4-n$.
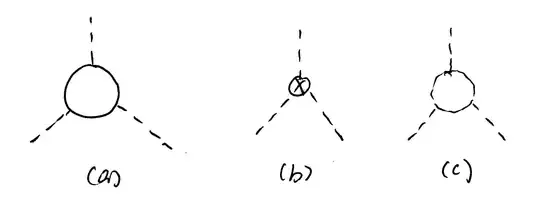
Suppose $n= 3$, I can draw this divergent diagram, with the counterterms (a) and (b):
If I now add another term $g_3\phi^3$ to this Lagrangian, we can draw another divergent graph (c) with the same superficial degree of divergence. My question is does the counterterm stay the same if I add this term? I'm not quite sure how to make sense of this.
Actually, with $n = 2,3,4$, we will have this same question. Is it right if I say the 1-loop correction for the $g\bar\psi\psi$ term leads to the need of counterterms for $\phi^2$, $\phi^3$, and $\phi^4$?