Penrose diagram of hypothetical astrophysical white hole

Question

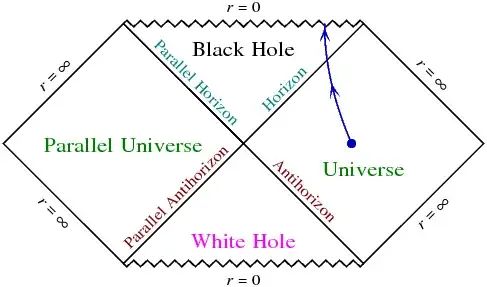
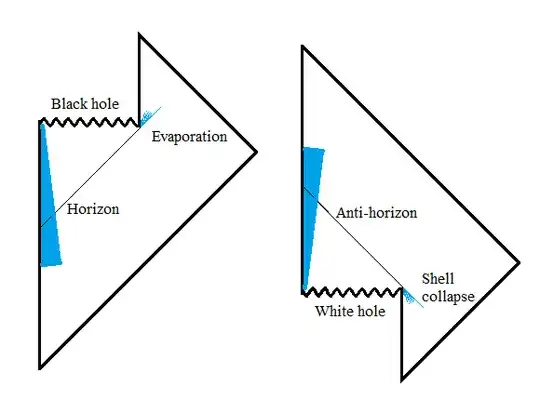
Assuming classical physics (no Hawking radiation), spherical symmetry, and no charge, Penrose diagrams are well known for the maximally extended Schwarzschild solution, for the theoretical (not maximally extended) black hole, and for a real astrophysical black hole.

Maximally extended solution:

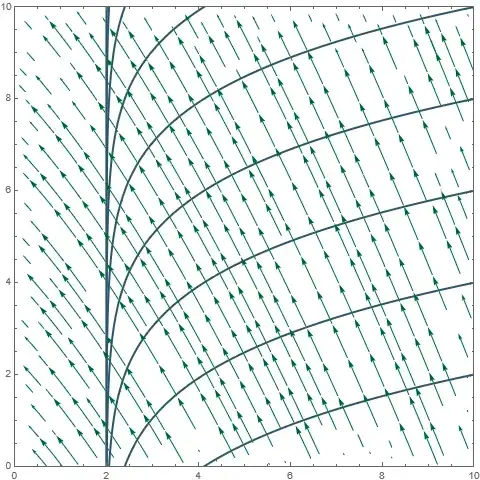
Theoretical (not maximally extended) black hole. It is easy to see that this diagram is the upper-right part of the diagram above for the maximally extended solution:

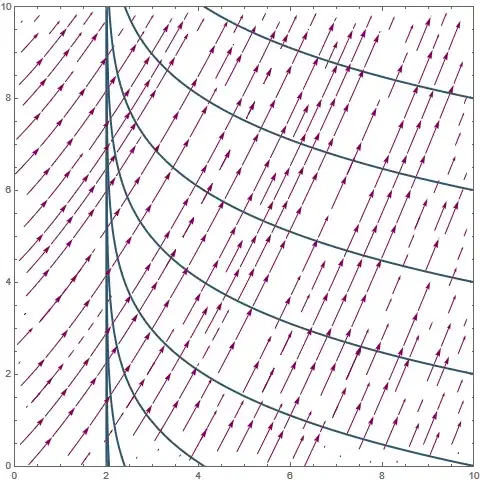
Astrophysical black hole:

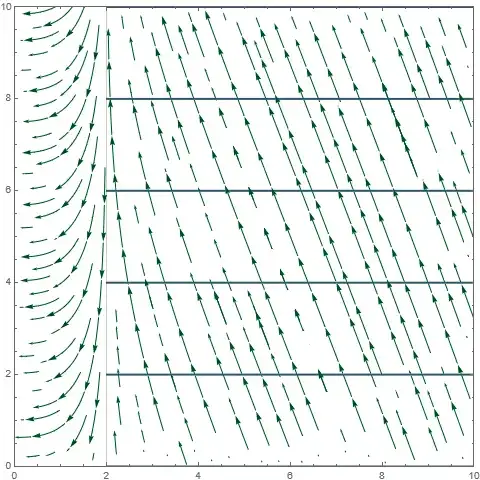
A white hole is a time reversed black hole with the same metric. We can easily plot a Penrose diagram for a theoretical (not maximally extended) white hole by vertically flipping the second diagram above. The result would look like the lower-right part of the first diagram above for the maximally extended solution.

The resulting diagram would represent a white hole that ho longer exists - nothing can fall toward it, although if it radiated in the past, we might still see its radiation.

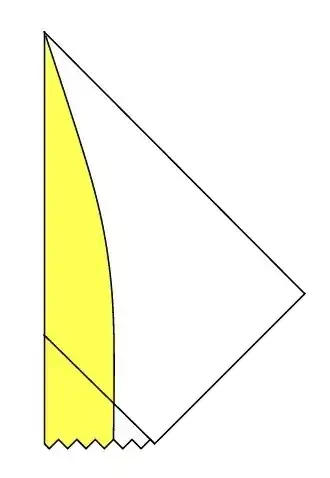
The full vertical flip represents the time reversal everywhere, both inside and outside the horizon. However, the Schwarzschild metric is time symmetric outside the horizon. Since reversing time outside does not change anything, we may not have to vertically flip the right part of the diagram outside the horizon. By keeping this part intact we should create a diagram of a white hole that still exists and can attract matter to fall toward it. (Please note that outside the antihorizon white holes attract matter exactly the same way as black holes do.)

It is however unclear how to time reverse the left part of the diagram (inside the horizon) without moving it down from the future to the infinite past.

While we are not aware of any physical process that could lead to the formation of white holes, we still can consider their hypothetical existence just as a thought experiment based on the math of the Schwarzschild solution. We also cannot completely rule out the existence of primordial black holes created by the Big Bang perhaps in a process that may not be fully understood (e.g. some Quantum Gravity process). This question is about such a hypothetical astrophysical white hole that could still exist somewhere and attract matter by its gravity.

I realize that light rays or objects falling to such a white hole cannot cross the antihorizon, so their geodesics must become incomplete by ending the proper time (or the affine parameter) at the antihorizon. This represents an asymmetry beyond the time reversal implying that the described procedure may be invalid and thus the existence of such white holes may be impossible even hypothetically.

QUESTION: What is a Penrose diagram of a hypothetical astrophysical white hole, not the theoretical one that exists in the infinite past, but the one that still exists (e.g. primordial) and can attract matter?

(CLARIFICATION: This question is not about the maximally extended solution.)

Or must all hypothetical white holes exist only in the infinite past without a possibility of any matter falling toward them?

Answer 1

safesphere asked: "This question is about such a hypothetical astrophysical white hole that could still exist somewhere and attract matter by its gravity."

A white hole on the Kruskal Szekeres and Carter Penrose diagrams always has the shape of a past light cone, so it is in no timelike oberserver's future since their worldlines' angles on the diagram can not be greater than 45°.

safesphere asked: "The full vertical flip represents the time reversal everywhere, both inside and outside the horizon."

True, but since our universe only has an infinite future, but no infinite past, we get to the big bang singularity at t=-13.8 Gyr before we get to the white hole horizon at r=2, t=-∞, and that singularity has an angle which is spaceliker than the 45° of the white hole horizon so that all geodesics have to originate there.

safesphere asked: "Must all hypothetical white holes exist only in the infinite past without a possibility of any matter falling toward them?"

On the Eddington Finkelstein spacetime diagram for ingoing raindrop vectors and the curves of constant Schwarzschild time (the arrow tips show which way the proper time, or if we have photons the affine parameter, grows):

you see the Schwarzschild time going to t=+∞ at the black hole horizon, and below for the outgoing free fallers on the white hole horizon it goes to t=-∞:

If we look at the same situation in coordinates where the Schwarzschild timelines are constant and track the ingoing particles that go to t=+∞ and down again:

the time reversed process of the particles getting swallowed by the singularity is the singularity giving birth to particles that go to t=-∞ and up again:

At the singularity itself, the singularity is not a place with infinitely small size that lasts infinitely long, but a time of infinitely short duration that happens at an infinitely large place, where particles emitted up or back in time is just like particles emitted to the left or right.

The reason why the singularity emits particles that (in an infinitely old universe) emerge at the horizon in the infinite past (just like the particles getting swallowed by the black hole pile up at the horizon for an infinitely long Schwarzschild time) is that at least in general relativity there is nothing that forbids the reversed process of getting terminated at the singularity, which is getting born by the singularity.

user4552 wrote: "The white hole's singularity is a spacelike boundary that lies in the past of all observers, similar to the big bang singularity."

Wikipedia wrote: "The white hole event horizon in the past becomes a black hole event horizon in the future, so any object falling towards it will eventually reach the black hole horizon"

So no one whos proper time τ is future directed can go there, and for those hypothetical observers with reversed proper time the white hole in our infinite past is just a black hole in their future.

You can be born by the white singularity in a frame where it is not a place but a time (for the worldlines terminating there with infinite relative velocity it is, due to the relativity of simultaneity), in that case you can't go back to the moment of your birth, or you die at the black singularity, in that case it is in your future which you can not escape.

If we with our future directed proper time would travel towards r=2 we would encounter the black hole, not the white hole.

If our world lines were flatter than 45° on the Kruskal Szekeres and Carter Penrose diagrams we could reach the white hole since a velocity greater than light implies travelling into the past.

By the way, the image description on the left of the 2nd image in your question (where the time axis is drawn vertical and the space axis horizontal) is misleading, on that diagram r=2 and t=∞ are both 45°. Constant t and r are not the axes but curves in a Penrose diagram, see here.

Answer 2

By keeping this part intact we should create a diagram of a white hole that still exists and can attract matter to fall toward it. (Please note that outside the antihorizon white holes attract matter exactly the same way as black holes do.)

There is some confusion here over what you mean by "still exists". The black hole singularity and white hole singularity are parts of the same maximally-extended eternal black hole solution. The gravity felt outside a black hole is due to the distribution of matter in the past. For an astrophysical black hole, this is the matter of the collapsing star. The gravity 'propagates' at the speed of light at $45^\circ$ up the diagram, so the curvature of space it causes remains even after the matter sourcing it has passed the horizon and hit the singularity, and no longer exists. ('Before' and 'after' are undefined for spacelike-separated events, so in the case of hitting the singularity I mean 'after' in the sense of being further up the diagram, vertically.)

The 'white hole' solution just pushes the source matter back in time as far as it will go. Instead of a collapsing ball of normal matter at some finite distance back in time, the mass giving rise to the black hole's gravity is concentrated in an eternal infinitely-dense singularity starting in the infinite past. But it is exactly the same as any other black hole in that the gravity arises from the distribution of matter in the past, and continues to exist after the matter that gives rise to it no longer does.

If you consider the 'black hole' to be the gravitational field outside the horizon, then it continues to exist. If you consider the 'black hole' to be the matter that gave rise to the gravitational field, then for any black hole it very quickly no longer exists. (And the future singularity doesn't yet exist, either.) The matter giving rise to the gravity maybe fell into the hole billions of years ago, or is stuck behind an event horizon from the infinite past. You appear to be using 'still exists' in the latter sense, although everyone else uses it to talk about 'black holes' in the former sense.

While we are not aware of any physical process that could lead to the formation of white holes, we still can consider their hypothetical existence just as a thought experiment based on the math of the Schwarzschild solution.

White hole creation is the time-reversal of black hole destruction. So consider the case of a black hole evaporating, and time-reverse it. For this, we take the burst of radiation and gravitational waves exploding out of the final evaporation of a black hole singularity, and time-reverse it to create a collapsing shell of radiation and gravitational waves converging on a point.

We can easily take the Penrose diagram of an evaporating astrophysical black hole and time-reverse it. The result shows a collapsing shell of radiation forming a singularity, which disgorges all the matter in the time-reversal of the collapsing star at its other end.

The causality that could give rise to this situation is unclear - instead of setting boundary conditions in the past and seeing what will subsequently happen, here we have to set future boundary conditions and ask what past events could give rise to that state. It seems likely that it's going to require us to violate the 2nd law of thermodynamics, and therefore be very difficult to engineer. So it's still theoretical.

QUESTION: What is a Penrose diagram of a hypothetical astrophysical white hole, not the theoretical one that exists in the infinite past, but the one that still exists (e.g. primordial) and can attract matter?

The Penrose diagram for a hypothetical astrophysical white hole resulting from the collapse of radiation corresponding to a time-reversed black hole evaporation is given above. However, the one that exists in the infinite past is primordial. In all cases the black hole (understood as the gravitational field) does still exist, even when the matter giving rise to it does not, and they all attract matter.

Answer 3

This answer is not directly addressing your question. But your comments indicate that your question is based on a more fundamental misunderstanding here. I understand this is probably not the proper method for addressing it around here (and I'll not debate it any further after this), but I hope you will find it more useful.

I am not asking about the maximally extended solution, but about a regular Schwarzschild solution reversed in time.

They are the same thing.

There is only one eternally static, spherically-symmetric solution to Einstein's equations for a point mass in a vacuum, and it involves all four quadrants of the diagram. Its time-reversal is identical. Historically, it so happens that because of the coordinates Schwarzchild used he only found a part of it, and it is also true that you can find one of the parts he missed by time-reversing the part he did find. But the part he found does not work as a solution on its own because there is nothing there to attract the matter. The future singularity is in the future, and the future cannot affect the past. Matter outside the black hole can only be attracted by the past singularity.

The past singularity and the event horizon around it are the source of gravity for the black hole, but because this part of the diagram only allows matter out, not in, people decided to call it a 'white hole' instead. But it isn't a distinct type of object to a black hole - it is part of the black hole. It is the gravitating mass in a black hole you are actually being attracted by.

Finally, your Penrose diagram shows a past white hole that cannot attract matter.

Yes, it can.

Matter can only be gravitationally attracted by matter in its past light cone. Otherwise you could use gravity to signal faster than light.

The conventional description of the Schwarzchild black hole can be confusing. While you are being pulled towards the future singularity, and end up there, you are not being pulled by the future singularity. The future hasn't happened yet.

We are used to the idea that the massive body we are pulled inwards by, and which we eventually hit, should be singular. For planets and stars, we have only one branch of the hyperbola to worry about. But past the horizon, the hyperbola splits into two branches: past and future. We can only see the past, we can only approach the future. The two roles are separated. It's highly counter-intuitive.

It is much the same situation as for the classic question: "If the sun disappeared, how long would it be before we knew about it?" The Earth sees the sun as it was 8 minutes ago. If the sun disappeared, the Earth would continue to orbit the empty space for another 8 minutes before the expanding gravitational wave cancelled the centripetal attraction and the Earth got flung out of orbit. Gravitational changes propagate at the speed of light. The Earth would still feel the gravity of the sun, for as long as it can see it, even after it has ceased to exist. In the same way, an astronaut orbiting a black hole still feels the gravity of the past singularity, even after it has ceased to exist.

Answer 4

The definition of a black hole can be written in English as

A black hole is region of spacetime that is not in the causal past of any outside observer.

The definition of white hole is the time reverse of this definition,

A white hole is a region of spacetime that is not in the causal future of any outside observer.

This immediately raises some ambiguity about what it would mean for a white hole to "still exist" in the same way that there is some ambiguity over whether a black hole can "ever" form. Ultimately, normal English is not well equipped to deal with the subtleties of ambiguous simultaneity.

If we exist on the white hole having spherical symmetry and being stationary, then the exterior has to be the normal Schwarzschild solution, and the only place it can go is behind the past horizon of the Penrose diagram of the Schwarzschild exterior.

If we want to look at the ultimate fate of a white hole, considering possibly non-stationary solitions, we run into additional trouble. The Penrose-Hawking singularity theorems guarantee (with the usual fine print involving energy conditions) that if we have white hole horizon in a spacetime, there must be a singularity to the past of this horizon. Since the laws of physics do not tell us anything about how this singularity is supposed to behave, we cannot say what will happen without making assumptions about the singularity emits.

The simplest assumption: nothing comes out of the white hole, will just produce the vacuum evolution of the solution. In the case of a spherically symmetric (uncharged) white hole this will just the maximally extended Schwarzschild solution (or at least the right hand side of its Penrose diagram. I.e. the white hole turns into a black hole in its future.

Of course, we can also assume that overtime the singularity in the white hole emits its entire mass in matter over its "life". In this case the white hole "evaporates" and the Penrose diagram for this will look the time reverse of the diagram for matter collapsing to a black hole, which in the spherical case again looks something like the flip picture from the OP:

We could consider various other scenarios, where the white emits only parts of its mass (and forms a smaller black hole), or emits a net amount of angular momentum (and forms a rotating black hole). We could even consider the case where the white hole emits more than its mass in matter (and forms a negative mass naked singularity). But in all cases we end up with the white hole existing in "the past" of the Penrose diagram. Essentially, what happens is that the definition of white hole fixes the structure of Penrose diagram near past timelike infinity to take a certain form.