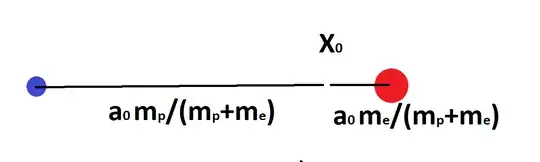According to various other answers on this site, most seem to feel that the Bohr Radius is the most accurate size of the hydrogen atom assuming this is defined as the radius where the electron is most often. This would seem to be contradicted by https://en.wikipedia.org/wiki/Bohr_radius which includes a section on reduced mass effects. So which is correct, the Bohr Radius or the version with reduced mass?
1 Answers
In the following text I explain how to properly understand this controversy. It's a bit of a pedantic discussion if I'm being honest.
When we properly solve the Schrodinger equation with a two-body Hamiltonian describing the motion of the electron and the proton, we get the following wavefunction (taken from the hydrogen atom wiki). This is described a bit more in my answer linked here. $$ \psi_{1s}(\mathbf{x})=\frac{1}{\sqrt{\pi}a_0^{3/2}}e^{-|\mathbf{x}|/a_0} $$ Where $a_0$ is $4\pi\epsilon_0\hbar^2/e^2\mu$, where $\mu$ is the "reduced mass" $m_em_p/(m_p+m_e)\approx m_e$. If you instead define the Bohr radius as $4\pi\epsilon_0\hbar^2/e^2 m_e$ (which I believe is the ordinary accepted definition), then yes there is absolutely a small correction. It's about 0.05%, so I presume this is what wikipedia is referring to.
But more detail is in order in my opinion to correctly describe what we're saying here. $\mathbf{x}$ is the difference in position between the electron and the proton: $\mathbf{x}=\mathbf{x}_e-\mathbf{x}_p$. If you found a way to measure $r=|\mathbf{x}|$, the difference in position between the proton and the electron, the most likely outcome would be $a_0$. You can observe this by plotting $r^2e^{-2r/a}$.
The full wavefunction for the entire atom can be written most conveniently with two parameters, $\mathbf{x}$, the position difference, and $\mathbf{X}$, the center of mass position
$$\mathbf{X}=\frac{m_e\mathbf{x}_e+m_p\mathbf{x_p}}{m_e+m_p} $$ A general wavefunction describing a hydrogen atom where the electron is in the groundstate is: $$ \psi(\mathbf{X},\mathbf{x})=\psi_{\text{free}}(\mathbf{X})\psi_{1s}(\mathbf{x}) $$ Where $\psi_{\text{free}}$ is a free-particle wavefunction. So assuming there is nothing for the hydrogen atom to interact with, the motion of the atom as a whole is that of a free particle. Energy eigenstates of this free particle system are plane waves filling all of space.
Depending on what you mean by "the radius of the electron," yet another correction may be in order. Suppose we just measured the position of the center of mass of the atom as a whole (not sure how we did that experimentally) and we got the result $\mathbf{X}_0$. Then the wavefunction is:
$$ \psi(\mathbf{X},\mathbf{x})=\sqrt{\delta(\mathbf{X}-\mathbf{X}_0)}\psi_{1s}(\mathbf{x}) $$
Then immediately after this first measurement (soon enough that the distribution of $\mathbf{X}$ hasn't had time to expand), we measure $\mathbf{x}$. The most likely outcome for $\mathbf{x}$ is $a_0$, but since $\mathbf{X}$ must be at $\mathbf{X}_0$, if $\mathbf{x}$ is measured to be $a_0$, then the distance from $\mathbf{x}_e$ to $\mathbf{X}_0$ is $a_0m_p/(m_e+m_p)$ and the distance from $\mathbf{x}_p$ to $\mathbf{X}_0$ is $a_0m_e/(m_e+m_p)$
- 8,778