For example, if we take a rod of mass $M$ and length L pivoted at one end and free to rotate about it. A body of mass M strikes the other end of rod, initially at rest perpendicularly with velocity v and e=0.what can we say about the velocity after collision. Is it also v or are there some other factors making it different from its linear cases.
1 Answers
Of course, $\epsilon$ is important for any collision. And you need to understand that all collisions happen in 1D along a line of action (typically called the contact normal).
In general, any 2D or 3D problem of contact between two free floating bodies with or without rotations comes down to the following steps
Find the impact speed $v_{\rm imp}$. That is the component of relative velocity along the line of action. The direction vector of the contact normal is $\boldsymbol{n}$, and the relative velocity vector is $\boldsymbol{v}_{\rm rel} = \boldsymbol{v}_1 - \boldsymbol{v}_2$. Then the impact speed is
$$v_{\rm imp} = \boldsymbol{n} \cdot (\boldsymbol{v}_1 - \boldsymbol{v}_2) \tag{1}$$
where $\cdot$ is the vector dot product.
Find the reduced mass $m^\star$. This is the linear mass the contact feels along the line of action. It combines the geometry and mass properties of all the bodies involved. if the individual body masses are $m_1$ and $m_2$ and their mass moment of inertia tensor about their center of mass ${\rm I}_1$ and ${\rm I}_2$. Also the location vectors of each center of mass from the point of contact are $\boldsymbol{d}_1$ and $\boldsymbol{d}_2$.
$$m^\star = \left( \tfrac{1}{m_1} + \tfrac{1}{m_2} + \left(\boldsymbol{n}\times\boldsymbol{d}_1\right)\cdot{\rm I}_1^{-1}\left(\boldsymbol{n}\times\boldsymbol{d}_1\right) \right)^{-1} \tag{2}$$
where $\times$ is the vector cross product. Also note that bold quantities are vectors, upright quantities are matrix (tensor), and italicized quantities are scalar variables.
Find the impulse magnitude $J$ of the impact. This part uses the above information and the coefficient of restitution $\epsilon$ into one simple equation $$J = (1+\epsilon)\, m^\star\, v_{\rm imp} \tag{3}$$
Apply the impulse to each body to modify the motion. The impulse magnitude $J$ is applied along the contact normal $\boldsymbol{n}$ and through the point of contact on each body to modify the motion of the center of mass in the following ways
$$ \begin{aligned} \Delta \boldsymbol{v}_1 & = - \tfrac{1}{m_1} \boldsymbol{n} J \\ \Delta \boldsymbol{\omega}_1 & = -{\rm I}_1^{-1} (-\boldsymbol{d}_1) \times \boldsymbol{n} J \\ \Delta \boldsymbol{v}_2 & = + \tfrac{1}{m_2} \boldsymbol{n} J \end{aligned} \tag{4}$$
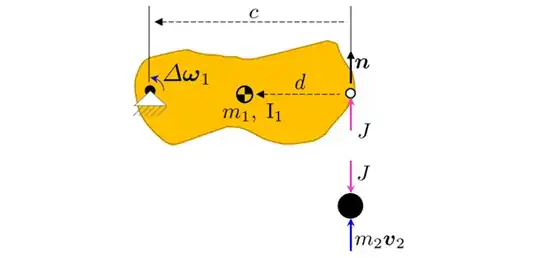
Now specifically the problem you mention is different because one end of one body is constrained to the ground through the pivot joint.
The same process as I outlined above applies, with only one modification. The calculation in (2) for the reduced mass $m^\star$ needs to be modified because the inverse mass moment of inertia ${\rm I}_1^{-1}$ is for a free-floating body, and the body is constrained by a pivot.
The new calculation is
$$m^{\star}=\left( \left(\boldsymbol{n}\times\boldsymbol{c}_{1}\right)\cdot\left(\boldsymbol{\hat{z}}\odot\boldsymbol{\hat{z}}\right)\left({\rm I}_{1}^{c}\right)^{-1}\left(\boldsymbol{n}\times\boldsymbol{c}_{1}\right)+\tfrac{1}{m_{2}} \right)^{-1} \tag{5}$$
where $\boldsymbol{c}_1$ is the location of the pivot relative to the contact point, and ${\rm I}^c_1$ is the mass moment of inertia tensor at the pivot after the parallel axis theorem is applied. Also $\odot$ is the outer product, and $\boldsymbol{\hat{z}}$ is the direction of the pivot.
One way of calculating the parallel axis theorem in 3D is by using the following $\cdot$ inner product and $\odot$ outer product summation $ {\rm I}_{1}^{c}={\rm I}_{1}+m_{1}\left(\left(\boldsymbol{c}_{1}-\boldsymbol{d}_{1}\right)\cdot\left(\boldsymbol{c}_{1}-\boldsymbol{d}_{1}\right){\bf 1}-\left(\boldsymbol{c}_{1}-\boldsymbol{d}_{1}\right)\odot\left(\boldsymbol{c}_{1}-\boldsymbol{d}_{1}\right)\right) $ and also ${\bf 1}$ is the identity matrix.
Since the kinematics are different with a pivoted body, equation (4) would need to modified. The thing to recognize here is that the impose $J$ are the contact point is going to cause a reaction impulse $\boldsymbol{R}$ at the pivot. The final effect on the motion including the effects of the pivot reaction are:
$$ \begin{aligned}\Delta\boldsymbol{v}_{1} & =\left(\boldsymbol{c}_{1}-\boldsymbol{d}_{1}\right)\times\left({\rm I}_{1}^{c}\right)^{-1}\left(\boldsymbol{c}_{1}\times\boldsymbol{n}\right)J\\ \Delta\boldsymbol{\omega}_{1} & =\left({\rm I}_{1}^{c}\right)^{-1}\left(\boldsymbol{c}_{1}\times\boldsymbol{n}\right)J\\ \Delta\boldsymbol{v}_{2} & =+\tfrac{1}{m_{2}}\boldsymbol{n}J \end{aligned} \tag{6}$$
In summary, the part you are asking, step (3) applies regardless of the nature and geometry of the problem. The coefficient of restitution $\epsilon$ changes the magnitude of the impulse between $1 \ldots 2$ times the value calculated by $m^\star v_{\rm imp}$.
The geometry and type of problem changes the mass the contact feels $m^\star$ ( reduced mass) with either equation (2) for free-floating bodies or equation (5) for constrained bodies.
If a body is a point mass, then anything containing the mass moment of inertia ${\rm I}_i$ is ignore and committed, just like the case for $m_2$ above.
Taking eq(5) from above in the 2D case you will find
$$ m^\star = \left( \tfrac{1}{m_2} + \tfrac{c^2}{I_z} \right)^{-1} $$
in contrast to eq(2) for the free-floating case where
$$ m^\star = \left(\tfrac{1}{m_1} + \tfrac{1}{m_2} + \tfrac{d^2}{I_z} \right)^{-1} $$
- 40,139