5

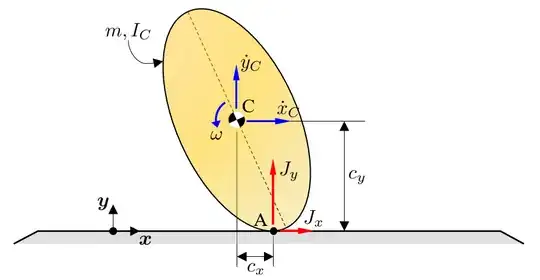
A prolate spheroid like a rugby ball or American football, dropped vertically with no rotation, will bounce vertically if it is oriented along one of it's axes of symmetry (in other words, if its centre of mass is directly above the point of impact on the ground).

However, if the ball is tilted some amount, the ball bounces with some horizontal component to its motion (as well as some angular velocity, but I'm not concerned with that for now).

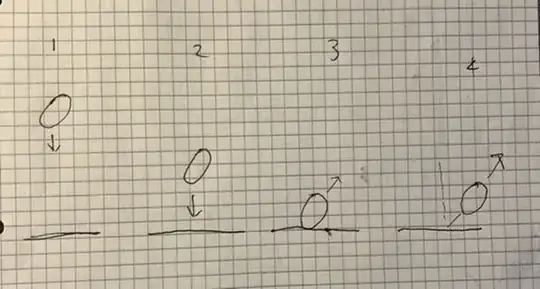enter image description here What's going on here to make this happen? At the point of impact, the normal force from the floor is of course purely vertical, so where does the horizontal component come from?

Intuitively, (and probably incorrectly) I have a picture in my head of a force being applied in a direction determined by the vector given by the point of impact on the ground and the centre of mass, but I think that's probably the wrong way to think about it.

Is the horizontal force coming from friction, that acts on the ball during the duration of its contact with the ground? I guess during the impact, the ball has a tendancy to want to push the point of contact away from the center of mass, in order for the center of mass to continue travelling downwards, and perhaps it's the friction in response to this that causes the horizontal component to the bounce?

Mark Morales II
  • 964
  • 1
  • 7
  • 15
Tom Davies
  • 153

2 Answers2

10

If the football is at an angle, the pointed end is not below the center of gravity. The point strikes the ground first. The ground pushes up on the point. This creates a torque that starts the ball rotating.

Since the point is on the ground, it may stick or dig in. Or there may be friction. The rotation may direct the point sideways, but forces from the ground push back. This sideways force on the ball give the ball a sideways velocity. When the ball bounces up, it is at an angle.

mmesser314
  • 49,702
6

The answer is because of friction.

Let us examine the moment of impact, with a simplified model of a 2D elliptical ball bouncing elastically off a horizontal plane, with the coefficient of restitution $\epsilon=1$, and coefficient of friction $\mu \gg 1$. The ball has mass $m$ and mass moment of inertia about the center of mass of $I_C$ in the plane of rotation (about a minor axis).

fig

In the diagram above all quantities are shown in their positive direction. The particular situation described in the question has zero horizontal velocity at the CM $\dot{x}_C=0$, negative vertical velocity $\dot{y}_C =-v_{\rm drop}$, as well as zero rotation $\omega=0$.

The result of the contact is two impulses $J_x$ and $J_y$ that result in the center of mass of the ball bouncing off at an angle. If there was no friction at the contact then $J_x=0$. With limited friction, you have $J_x \leq \mu J_y$.

$$ \begin{aligned}J_{x} & =-\left(1+\epsilon\right)\frac{c_{y}c_{x}}{\frac{I_{C}}{m}+c_{x}^{2}+c_{y}^{2}}\;mv_{{\rm drop}}\\ J_{y} & =\left(1+\epsilon\right)\left(1-\frac{c_{x}^{2}}{\frac{I_{C}}{m}+c_{x}^{2}+c_{y}^{2}}\right)\;mv_{{\rm drop}} \end{aligned}$$

The angle of the impulse $\psi$ (from vertical) can be found with

$$ \tan{\psi} = \frac{J_x}{J_y} = -\frac{c_x c_y}{\frac{I_c}{m} + c_y^2} $$

The side bounce effect exists because of the offset $c_x$ above and the presence of friction. Again, with not friction $J_x=0$ and the bounce angle would be zero (from vertical).

When measuring the resulting motion of the center of mass after the impact you will find the bounce angle as

$$ \tan{\theta} = \frac{v_x}{v_y} = (1+\epsilon) \frac{m c_x c_y}{m c_x^2 - \epsilon ( I_C - m c_y^2) } $$

which shows a strong dependency with the coefficient of restitution $\epsilon$. The limiting case of a plastic collision with $\epsilon=0$ results in $\tan{\theta} = \frac{c_y}{c_x}$ which is along the direction of the center of mass. As the bounciness increases, it also increases the angle $\theta$.

John Alexiou
  • 40,139